Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 07. 2011 15:42 — Editoval miso16211 (05. 07. 2011 15:45)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Logaritmická (původně Logsrytmicka) rovnica

x = ?
Neviem ako nato prísť.
Veď to je vlastne 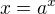

Offline
#2 05. 07. 2011 16:05
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Logaritmická (původně Logsrytmicka) rovnica
↑ miso16211:
Převeď si to na zlomek: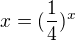
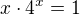
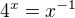
V kterém bodě se protíná funkce  a
a 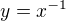 ?
?
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 05. 07. 2011 18:55
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Logaritmická (původně Logsrytmicka) rovnica
Fakt nevim jak nato prisť.
Offline
#4 05. 07. 2011 19:40
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Logaritmická (původně Logsrytmicka) rovnica
↑ miso16211:
No početně také nevím, ale odhadnout to lze, je to celkem pěkné číslo. je oproti
je oproti  velké číslo. Takže zkus čtyřku umocnit tak, abys to číslo zmenšil a naopak 1/x umocnit tak, aby se z toho stalo číslo větší jak jedna.
velké číslo. Takže zkus čtyřku umocnit tak, abys to číslo zmenšil a naopak 1/x umocnit tak, aby se z toho stalo číslo větší jak jedna.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#5 05. 07. 2011 20:58 — Editoval MartinK (05. 07. 2011 21:02)
Re: Logaritmická (původně Logsrytmicka) rovnica
Zdravím,
Nějak jsem odhadl, že .
Pak mě napadlo toto(možná to řeším příliš složitě):
Zlogaritmoval jsem to se základem :
Řešíme tedy rovnici, kdy potřebujeme zjistit, kdy se rovnají dvě inverzní funkce:
.
Tady jsem se ale zasekl. :)
EDIT: Jak tak koukám, tak to asi nikam nevede :)
Offline
#6 05. 07. 2011 21:07
Re: Logaritmická (původně Logsrytmicka) rovnica
Úloha by sa dala riešiť pomocou http://en.wikipedia.org/wiki/Lambert_W_function
1^6 - 2^6 + 3^6 = 666
Offline
#7 06. 07. 2011 16:22 — Editoval miso16211 (06. 07. 2011 16:23)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Logaritmická (původně Logsrytmicka) rovnica
nechapem jak možes napísať ↑ MartinK:
A to som ja vymyslel. resp. som robil zbierku na soč.
Offline
#8 06. 07. 2011 21:25 — Editoval found (06. 07. 2011 21:25)
Re: Logaritmická (původně Logsrytmicka) rovnica

Proto to může napsat, ale jak dál také netuším, zkoušel jsem i jiné postupy, ale ani wolfram nevyhodí nic plnohodnotného - jen řešení 1/2.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#9 06. 07. 2011 22:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Logaritmická (původně Logsrytmicka) rovnica
Zdravím vás,
rovnice tohoto typu nejde řešit pomocí "běžných postupů". Pokud se podaří zadání, potom lze kořen rovnice uhodnout - jak se podařilo v této úloze ↑ MartinK:.
Ovšem je třeba dokázat, že tento kořen je jediný - grafická metoda, která by se zde nabízela, mi byla striktně a správně zakázána a to opakovaně: přečtete si, prosím, komentáře Mariana - je to zlatý fond tohoto fóra:
http://forum.matweb.cz/viewtopic.php?pid=19#p19 - zde si všimnete časového rozdílu mezi příspěvky představitelů zlatého fondu. Ovšem kolegovi Kondrovi se návrh na použití grafu nezakázal - svět je nespravedlivý :-)
http://forum.matweb.cz/viewtopic.php?pid=64314#p64314
http://forum.matweb.cz/viewtopic.php?pid=16039#p16039
Tedy bych takovou rovnici do sbírky pro SŠ zařazovala jen opatrně a bylo by lepší uvést důvod, proč je taková rovnice zařazena.
Offline
#10 01. 01. 2012 19:35 — Editoval Matej1117 (02. 01. 2012 14:23)
Re: Logaritmická (původně Logsrytmicka) rovnica
neviem ci vam to nejako pomoze ale vsimol som si ze v takomto priklade musi pre x platit ze 0,25 je x-ta odmocnina z "x".
Sorry neviem pisat v tom programe ..
cize plati:
x=A^x
A= x^(1/x)
____________
x = 0,25^x
0,25 = x^(1/x)
Je zaujimave ze pre cisla vyssie ako 1 dosadene za A nema tato rovnica riesenie okrem cisiel 3^1/3, 4^0,25, 5^0,2, 6^1/6 atd.
Offline
