Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#101 10. 03. 2011 14:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
Zdravím vás,
není to nic podstatného - jen mám takový námět ohledně mazání duplicitních témat. Myslím, že je dostačující, pokud označíme za vyřešené a dame odkaz na duplicitu.
Není nutné nahlašovat Moderátorům - nahlašování je více pracné (než jen zafajfknutí) a Moderátory to ruší (neuvěřitelný potenceiál maji, můj obdiv). V označeném tématu už nikdo odpovídat nebude.
Pokud vážené Moderátorstvo popadne záchvat pořadkumilovnosti, tak pomocí tlačítka "Hledat" a kličového slova "duplicitní" jednou za čas taková temata najdou a uklidí.
EDIT: tak například.
Co si myslite? Děkuji.
---------------
Podstatné - má milá členka Claudia fajfkatko? Pokud ne - navrhuji přidělit - asi bude potřebovat uzavřit debatu. Zásluhy - dovršila výcvik budoucího meteorologa v použití TeX (pravda, kolega byl také velmi vstřicný a učenlivý :-)
Děkuji, nehoří.
Offline
#102 04. 10. 2011 11:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
Zdravím vás,
neuměla bych spolehlivě působit v tomto tématu - důkazové úlohy neovládám (a pomoci Rektoryse se to nastudovat nedá).
Pokud byste někdo našel čas a ochotu kolegovi poradit, zda se vydal správným směrem (viz 1. příspěvek), budu velmi vděčna. Moc děkuji.
Offline
#103 26. 10. 2011 22:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
Zdravím vás, určitě jde o standardní algoritmus - část "obdélník - obdelník" (tipuji originál úlohy) - neměli byste doporučení, děkuji :-)
Upraveno: vyřešeno v tématu, děkuji kolego Stýve.
Offline
#104 22. 04. 2012 12:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
Zdravím vás,
opakovaně jsem narazila na rozbor úlohy z Maturity 2011 - č. 12, máme i ve Vzorových v SŠ (řešiteli Hanisovi děkuji :-). V jednom z tématu (zkusím dohledat) se rovnou předpokládá, že posloupnost geometrická (což se mi nezdálo). Můžete se, prosím, podívat a upřesnit, zda tento předpoklad je možný a postup je korektní.
Děkuji.
Offline
#105 22. 04. 2012 12:12 — Editoval Pavel Brožek (22. 04. 2012 12:12)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nezodpovězené dotazy
↑ jelena:
Posloupnost  není geometrická, je to posloupnost částečných součtů geometrické posloupnosti. U Hanise se mi nelíbí jen řádek
není geometrická, je to posloupnost částečných součtů geometrické posloupnosti. U Hanise se mi nelíbí jen řádek
V závorce máme součet geometrických posloupností s koeficientem q. Pro každou GP platí, že je konvergentní právě tehdy, když
Spíš bych psal:
V závorce je částečný součet členů geometrické posloupnosti. Pro každou geometrickou řadu platí…
Offline
#106 22. 04. 2012 12:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
↑ Pavel Brožek:
děkuji, měla jsem jen matné vzpomínky, že se mi něco nezdálo a už tehdy jsem se chtěla zeptat - v tomto tématu. Potom kolega Peta8 vystavil na svůj web.
Tak teď nevím, na kterém místě se to má opravit, aby se dalo spolehlivě odkázat, pokud vůbec. Děkuji, nehoří.
Offline
#107 24. 04. 2012 20:20
Re: Nezodpovězené dotazy
↑ Pavel Brožek:
Jestli to dobře chápu, tak to slovo částečný součet používáš jen proto, že "n" dané posloupnosti je pak v případě součtu geometrické pro n-1.
Na té tvé opravě by se dalo najít víc nedostatků než na tom "obecném" originálu.
Offline
#108 24. 04. 2012 20:41 — Editoval Pavel Brožek (24. 04. 2012 20:42)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nezodpovězené dotazy
↑ peter_2+2:
Nedokázal jsem se úplně zorientovat v tvé připomínce, tak nevím, jestli odpovím, na co se ptáš.
„n-tý částečný součet“ so obvykle (s ničím jiným jsem se nesetkal) používá pro součet prvních n členů posloupnosti.
V tomto konkrétním případě jsem „částečným součtem členů geometrické posloupnosti“ myslel součet  , kde jednotlivé sčítance jsou členy geometrické posoupnosti
, kde jednotlivé sčítance jsou členy geometrické posoupnosti  , v součtu je n-1 prvních členů této geometrické posloupnosti, jde tedy o částečný součet. Kolikátý je to částečný součet jsem nepovažoval za nutné zmiňovat, proto jsem napsal jen částečný součet.
, v součtu je n-1 prvních členů této geometrické posloupnosti, jde tedy o částečný součet. Kolikátý je to částečný součet jsem nepovažoval za nutné zmiňovat, proto jsem napsal jen částečný součet.
Pokud tam mám nějaké nedostatky, tak je prosím napiš, nejsem si žádných vědom.
Offline
#109 24. 04. 2012 20:56
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nezodpovězené dotazy
Pro Hanise:
Všiml jsem si, že jsi první část citovaného textu opravil, ale druhou jsi nechal, jak byla.
V zadání se ptají na konvergenci posloupnosti  . To není geometrická posloupnost. Nemá tedy smysl, když na konci bodu 2.) píšeš „Pro každou GP platí, že je konvergentní právě tehdy, když
. To není geometrická posloupnost. Nemá tedy smysl, když na konci bodu 2.) píšeš „Pro každou GP platí, že je konvergentní právě tehdy, když  “. Sice je to pravda (když nebudeme považovat nulovou posloupnost za geometrickou posloupnost, tam pak může být q libovolné), ale neřeší to zadání. Vlastně tím říkáš, že limita členů geometrické posloupnosti v závorce je nula, což je ale pouze nutná podmínka kovergence toho částečného součtu. Je potřeba napsat, že geometrická řada (tj. posloupnost částečných součtů v závorce) je konvergentní pokud
“. Sice je to pravda (když nebudeme považovat nulovou posloupnost za geometrickou posloupnost, tam pak může být q libovolné), ale neřeší to zadání. Vlastně tím říkáš, že limita členů geometrické posloupnosti v závorce je nula, což je ale pouze nutná podmínka kovergence toho částečného součtu. Je potřeba napsat, že geometrická řada (tj. posloupnost částečných součtů v závorce) je konvergentní pokud  .
.
Offline
#110 24. 04. 2012 22:08
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Nezodpovězené dotazy
Ahoj,
původní příspěvek jsem psal před cca rokem, to jsem byl teprve třeťák. Nová formulace:
1.) beze změny
2.) ...
V závorce se objevuje geometrická řada s kvocientem q. Tato geometrická řada je konvergentní, pokud |q|<=1
3.) Pro q=-0,5 dostáváme:
Tato NGŘ je konvergentní, protože |q|=0,5<1, proto existuje součet: 

Povídej a opravuj, já to umím spočítat, ale nevím, jak to formálně napsat (sám nevím, jaký je rozdíl mezi geometrickou posloupností a geometrickou řadou).
Offline
#111 24. 04. 2012 22:56 — Editoval Pavel Brožek (24. 04. 2012 23:12)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nezodpovězené dotazy
↑ Hanis:
Ahoj,
2) pro |q|=1 není geometrická řada konvergentní (pro q=1 se totiž sčítá nekonečně stejných čísel, pro q=-1 řada „kmitá“ mezi dvěma hodnotami a proto říkáme, že nekonverguje).
3) To  bych vynechal, myslím, že tři tečky stačí. Sice je to takhle názorné, že to jde „až do nekonečna“, ale nepíše se to tak. Určitě bych si ale dal pozor na to psát
bych vynechal, myslím, že tři tečky stačí. Sice je to takhle názorné, že to jde „až do nekonečna“, ale nepíše se to tak. Určitě bych si ale dal pozor na to psát  ve smyslu toho prvního členu v závorce, protože
ve smyslu toho prvního členu v závorce, protože  už má v této úloze jiný význam (
už má v této úloze jiný význam (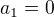 ).
).
Geometrická posloupnost je posloupnost čísel, např.  , geometrická řada je součet všech členů geometrické posloupnosti (přesně se řada definuje jako limita částečných součtů
, geometrická řada je součet všech členů geometrické posloupnosti (přesně se řada definuje jako limita částečných součtů  , kde
, kde  jsou tady členy geometrické posloupnosti), např.
jsou tady členy geometrické posloupnosti), např.  .
.
Také se mi geometrická posloupnost a řada ze začátky pletly :-).
Offline
#112 24. 04. 2012 23:10
#113 24. 04. 2012 23:14 — Editoval Pavel Brožek (24. 04. 2012 23:17)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nezodpovězené dotazy
↑ Hanis:
Nemáš zač, já děkuji za plusko :-).
Teď jsem jen zvědavý, s jakými věcnými připomínkami přijde Peter :-).
Offline
#114 25. 04. 2012 12:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
↑ Pavel Brožek:, ↑ Hanis:
:-) děkuji velice, silný týme. Kolega Zdeněk byl tak laskav a umístil řešení na MatWiki a prosí (to jsem přeložila z PM) Pavla, aby případně upravil technické detaily.
Já ještě prosím Pavla, zda by se nepodíval na kolegovo téma.
Pavel B. napsal(a):
Teď jsem jen zvědavý
To si, prosím, dohodnete a zvolte nějaké vhodné téma v jiné sekci - snad nebudete vyrušovat Vrchního Velitele z vybarvování Maturitní nástěnky (fakt, že zvýrazněna témata jsou neviditelná :-).
Opět s pozdravem "Svobodu stolům" (to snad není ani možné už :-)
Offline
#115 25. 04. 2012 16:43 — Editoval peter_2+2 (25. 04. 2012 16:48)
Re: Nezodpovězené dotazy
↑ Pavel Brožek:
Původně jsem to chtěl nějak zkrátit, ale když mě tak pobízíš tak to sem dám v původní velikosti.
Abych se přiznal tak to ozančení "částečný" neznám(ikdyž je nejspíš poměrně běžné), ale předpokládám, že to slovo "částečný" z něčeho pramení. Předpokládám tedy, že to je ta druhá varianta označení, která mě původně napadla(která mi ovšem také nedávala smysl a to možná ještě víc), což naznačuje i to co jsi napsal. Tedy, že slovo "částečná" pramení z toho, že pokud vytvořím novou posloupnost tak, že budu sumovat členy jiné posloupnostit, a to až po konkrétní "n",
Například
index(n) 1 2 3 4 5 6
1 1 1 1 1 1 (aritmetická posloupnost začínající a1=1 s diferencí d=0)
1 2 3 4 5 6 (v daném "n" jde o součet výš uvedené posloupnosti => řada přirozených čísel)
pak půjde o konečný "částečný" součet pro prvních "n" členů jinak "nekonečné posloupnosti".
Čili máš pravdu, že pokud je ten pojem "částečný" zavedené slovo, není potřeba specifikovat kde ta "část" začíná, to kde končí už není tak důležité, to máš určitě pravdu taky.
Ale u "n-2" sotva poznáš, že jde o částečný součet. Mimo to já bych mohl říct, že jde o součet této posloupnosti, a měl bych taky určitě pravdu:
A už by o částečný součet najednou nešlo, (tedy né pro ono n=nekonečno).
Čili předpokládám, že v tom slově částečný se vychází z toho, že "n" je konečné číslo zatímco původní posloupnost je nekonečná.
Potažmo jak by jsi tvrdil ty, číslo menší než "n". Samozřejmě by mohla vzniknout situace..., jak nazvat součet pro nekonečno a hlavně pak nekonečno mínus jedna členů, skoro bych si troufl to druhé ozančit za "skoro úplný součet" :). Ale stejně z té věty neplyne, že se to porovnává s "n".
Offline
#116 25. 04. 2012 17:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nezodpovězené dotazy
↑ peter_2+2:
Jsem rád, že mi v podstatě dáváš za pravdu :-). Ano, slovo částečný z něčeho pramení, konkrétně z toho, že nejde o součet všech členů posloupnosti, ale pouze jejich části.
Když se řekne n-tý částečný součet řady, tak se samozřejmě myslí n přirozené. Pokud uděláme limitu posloupnosti částečných součtů 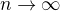 , pak ta limita už není částečný součet řady, ale součet řady.
, pak ta limita už není částečný součet řady, ale součet řady.
Offline
#117 26. 04. 2012 15:38
Re: Nezodpovězené dotazy
↑ Pavel Brožek:
To jsi si vysvětlil dost po svým dá se říct. Zkrátka to tvoje upřesnění je jen jakási definice tvé představy, že posloupnost, o které mluvíš, která tam není navíc ani uvedena, je nekonečná nebo je konečná a má členů víc než příslušná suma v závorce. (posloupnost nemusí být nutně nekonečná)
A to celé navíc ještě za předpokladu, že "n" není nekonečno, což v případě té limity je.
Offline
#118 26. 04. 2012 19:32
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nezodpovězené dotazy
↑ peter_2+2:
Ta moje představa je (troufám si tvrdit) obecně přijímaná představa a každý, kdo má základy kolem posloupností a řad, jistě správně pochopí to, co jsem napsal, bez dalšího upřesňování představ.
n v případě limity není nekonečno. Provádí se limita, kde n jde do nekonečna. n je ale vždy konečné přirozené číslo. Symbol nekonečna se pouze používá na mnoha místech jako zkratka, ale nepředstavuje zde žádné číslo.
Myslím, že už si rozumíme dostatečně na to, abychom debatu mohli ukončit.
Offline
#119 28. 04. 2012 13:19 — Editoval peter_2+2 (28. 04. 2012 13:19)
Re: Nezodpovězené dotazy
↑ Pavel Brožek:
No ja myslím, že to ukončím tím, že kdekoliv jsem na internetu hledat parital sum of sequence, tak jsem toto slovo nikde neviděl použít, anižby bylo řečeno, z čeho je daná partial sum, takže se nejspíš ani nejedná o samostatný pojem (mimo to proč to slovo "částečný" nejde použít samostatně, jsem už doufám vysvětlil dostatečně)
Taky jsem při tom hledání narazil na definici řady... není definovaná pomocí posloupnosti, která vznikne sumací jiné (posloupnost částečných součtů jiné posloupnosti), nýbrž je definovaná samostatně:
Offline
#120 28. 04. 2012 13:21
Re: Nezodpovězené dotazy
↑ peter_2+2:
Píšeš nesmysly. Raději bys měl to úsilí vrhnout do učení se matematiky, než do etymologického zkoumání matematiky.
What does a drowning number theorist say?
'log log log log ...'
Offline
#122 24. 06. 2012 21:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
Zdravím,
prosím Pavla B. (nebo Pavlova spolužáka) zda by se nepodíval(i) na téma spolužačky a vnesl(i) jasno. Může se podívat a vnést jasno i někdo další z kolegů (přípravnou práci jsem provedla). Děkuji :-)
doplněno: děkuji, vyjasněno :-)
Offline
#123 05. 08. 2013 11:50 Příspěvek uživatele ricola1 byl skryt uživatelem ricola1.
#124 25. 11. 2013 08:46
#125 14. 12. 2013 17:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nezodpovězené dotazy
Zdravím,
mohla bych poprosit někoho z místních statistiků a ekonometrů o zkontrolování, zda jsme správně pochopili zadání a postupujeme smysluplně. Děkuji.
Offline