Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#101 14. 06. 2012 12:12 — Editoval vanok (23. 06. 2012 17:01)
Re: najkrajsia teorema
Ako mi poradili kolegovia, otvoril som specialne vlakno pre toto zabavne cvicenie
http://forum.matweb.cz/viewtopic.php?pid=295073#p295073
EDIT: Tak uz je to dokazane, a mozete si tam precitat dokaz od kolegu OiBobik-a, ako aj moj.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#102 21. 06. 2012 00:10
Re: najkrajsia teorema
Michael Atiyah, Fields-ova medaila 1966
tu hovori o KRASE V MATEMATIKE
http://video.google.com/videoplay?docid … 8813393554
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#103 22. 06. 2012 20:05 — Editoval vanok (23. 06. 2012 17:07)
Re: najkrajsia teorema
Tento vysledok je (podla mna velmi pekny)
Nech 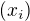 su vsetky pozitivne korene rovnice
su vsetky pozitivne korene rovnice  uporiadane stupajuco.
uporiadane stupajuco.
Mame 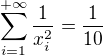 .
.
Davam ho tu bez dokazu, ale ak niekto mysli, ze
si s tym moze poradit, nech nevaha, dat svoje riesenie tu
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#104 25. 06. 2012 22:59 — Editoval vanok (30. 06. 2012 12:17)
Re: najkrajsia teorema
Dnes tu davam zaujimavu poznamku, o peknej metode ako vypocitat sucet nejakej rady vdaka vete o residus.
Na vypocet suctu rady vseobecneho clenu  , musime vyjadrit tuto radu ako sucet residus jednej funkcie. Pre kazde cele n, treba vyjadrit clen
, musime vyjadrit tuto radu ako sucet residus jednej funkcie. Pre kazde cele n, treba vyjadrit clen  tak aby bol residu pre
tak aby bol residu pre  nejakej funkcie viazanu na
nejakej funkcie viazanu na 
Preto pouzime funkciu 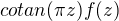 kde
kde 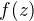 je definovana ako
je definovana ako  , kde nahradime celu premenu
, kde nahradime celu premenu  , komplexnou premenou
, komplexnou premenou  (kde
(kde 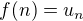 )
)
Tato metoda, sa zda byt umela,ale ked si uvedomime ze jej singularity su cele relativne cisla  lebo
lebo 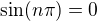 a naviac
a naviac 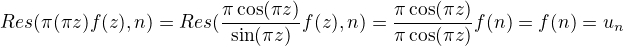
Preto sucet residus je sucet radu  . Ostava nam este definovat uzavretu krivku vo vnutri ktorej su vsetki body
. Ostava nam este definovat uzavretu krivku vo vnutri ktorej su vsetki body  , a konecne vypocitat hodnotu integralu.
, a konecne vypocitat hodnotu integralu.
Poznamka: pridam tu este jeden konnretny priklad, len co budem mat viac casu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#105 27. 06. 2012 14:58 — Editoval vanok (27. 06. 2012 15:06)
Re: najkrajsia teorema
Tak ten slubeny priklad ↑ vanok:
Vypocitajte sucet rady 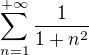
Na vypocet tohto suctu uvazujme nasledujuci integral: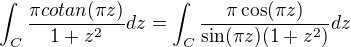
kde  je obvod stvorca daneho jeho vrcholmy:
je obvod stvorca daneho jeho vrcholmy: 
Poly funkcie 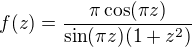
su vsetki cele cisla  , take ze
, take ze 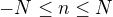 a
a  ( odmocniny cisla
( odmocniny cisla  )
)
Veta o residus nam da 
vypocitajme vsetki residus


Po dosadeni mame .
.
Ostava nam vypocitat integral:
zvysok dokoncim neskor
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#106 29. 06. 2012 20:34 — Editoval jelena (30. 06. 2012 15:26)
Re: najkrajsia teorema
Pokracovanie a koniec slubenych vypoctov.
Na vypocet integralu pouzijeme nerovnosti na obvode stvorca vrcholov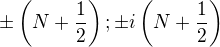 kde
kde  je cele cislo..
je cele cislo..
Tento stvorec, orientovany positivne obsahuje body  , kde
, kde 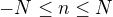 .
.
Lahko ukazeme rovnost: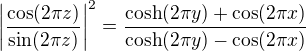
Na zvyslych stranach stvorca, ktore oznacime 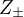 mame
mame  , a tak
, a tak 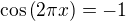
co nam da:
Naviac mame tuto nerovnost:
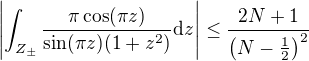
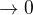 pre
pre 
Podobne na vodorovnych stranach mame, ktore oznacime 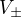 mame:
mame: .
.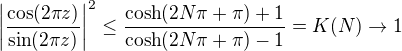 pre
pre 
Na koniec 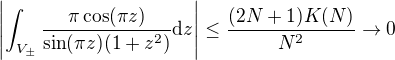 pre
pre 
Cize sme dokazali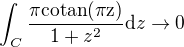 pre
pre 
co nam okamzita da
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#107 29. 06. 2012 21:16 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: oprava TeX - vyřešeno
#108 29. 06. 2012 21:36 Příspěvek uživatele vanok byl skryt uživatelem jelena. Důvod: oprava TeX - vyřešeno
#109 29. 06. 2012 21:41 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: oprava TeX - vyřešeno
#110 29. 06. 2012 22:01 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: oprava TeX - vyřešeno
#111 29. 06. 2012 22:09 — Editoval vanok (29. 06. 2012 22:22) Příspěvek uživatele vanok byl skryt uživatelem jelena. Důvod: oprava TeX - vyřešeno
#112 30. 06. 2012 00:52 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: oprava TeX - vyřešeno
#113 06. 07. 2012 13:14
Re: najkrajsia teorema
Pozdravy vsetkym.
Tu som dal jeden dokaz tykajuci sa Bell-ovych cisiel
http://forum.matweb.cz/viewtopic.php?pid=298085#p298085
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#114 14. 07. 2012 15:51 — Editoval vanok (15. 07. 2012 15:33)
Re: najkrajsia teorema
Vynimka:
nejde mimoriadne o nieco matematicky najkrajsie.
Ale nieco GENIALNE pre LaTeX 
http://detexify.kirelabs.org/classify.html
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#115 18. 07. 2012 08:47 — Editoval Andrejka3 (18. 07. 2012 08:55)
Re: najkrajsia teorema
Ahoj.
Na procházce jsem narazila na tuhle hru
What does a drowning number theorist say?
'log log log log ...'
Offline
#116 18. 07. 2012 10:06
Re: najkrajsia teorema
Ahoj ↑ Andrejka3:,
Tato varianta HRA NIM (jednoduchsia) bola do hlbky studovana
http://en.wikipedia.org/wiki/Nim
http://fr.wikipedia.org/wiki/Jeux_de_Nim
Mozno porovnat obe HRY by bolo zaujimave.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#117 25. 07. 2012 23:34
Re: najkrajsia teorema
Toto je pekna tema
http://forum.matweb.cz/viewtopic.php?id=48971
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#118 28. 07. 2012 12:17 — Editoval vanok (07. 08. 2012 13:57)
Re: najkrajsia teorema
Pojem UHOL.
Otvoril som nove vlakno na tuto temu.
Je to iste zajuimave mat odpovede na tuto temu.
Podla mna opdoved je zavisla na urovni:
Zakladna skola,
prve rocniky
posledne rocniky
Stredna skola
Vysoka skola.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#119 28. 07. 2012 16:48
Re: najkrajsia teorema
↑ vanok:
To jsem tedy zvědavá, kam to povede. S tím pojmem mám velké problémy - kdysi jsem se snažila o nějakou axiomatizaci, že bych se dostala k úhlu, ale nikdy to nebylo uspokojivé. A tak mám pocit, že všechno jde do kruhu a nikde není pořádně napsané, co z čeho plyne.
What does a drowning number theorist say?
'log log log log ...'
Offline
#120 28. 07. 2012 20:36
Re: najkrajsia teorema
Ahoj ↑ Andrejka3:,
Ano uplne z tebou suhlasim.
Povedal by som, ze definicie, co poznam, su ale priliz strucne (dokonca niekedy aj nepresne) alebo priliz pedantna.
V prispevku #118 doeditujem moznu odpoved na kazdu uroven...
Iste potom vyjadris tvoj nazor.
Ale nevahaj reagovat vo specialnom vlakne co som otvoril.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#121 03. 08. 2012 09:34
Re: najkrajsia teorema
↑ vanok:, ↑ Andrejka3:
Ahoj. Způsob definice bude záviset i na tom, co chceme pojmem "úhel" vyjádřit: zda množinu bodů ohraničenou dvěma polopřímkami
se společným počátkem nebo vzájemný "metrický" vztah takových polopřímek.
Offline
#122 03. 08. 2012 11:57
Re: najkrajsia teorema
↑ Rumburak:
Pozdravujem, v prispevku #118, som zacal malu syntezu na tuto temu
Postupne to popridavam sem. A dam odkazy aj do temy co som otvoril na tento ucel.
Ked to dokoncim, iste sa nam bude lepsie diskutovat napriklad na tejto baze.
Dakujem, ze sa zaujimas o tuto temu.
Pekny WE
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#123 13. 08. 2012 18:07
Re: najkrajsia teorema
Mala uvaha o troch geometriach: Euklidovska, afinna, projektivna a ich invariatnych transformaciach.
Euklidovska geometria je taka, ze ich grupa invariatnych trasformacii, respektuje vzdialenost... a naviac aj uhly ( ale opacne tvrdenie neplati, lebo napriklad homografie respectuju uhly ale nie vzdialenosti)
Pridam tu neskor priklady nejakych euklidovskych problemov.
Afinna geometria je taka, ze ze jej grupa invariantov, konservuje pomer
Napriklad, prostriedok usecky ...
Aj tu pridam nekor nejake take priklady
Projektivna geometria je taka, ze ze jej grupa invariantov, konservuje dvojpomer dlzok... a priamky (kolinearitu)
Tu tiez pridam nekor nejake take priklady
Poznamka: Na tuto ( peknu temu) budem pokracovat, len ak budu uz na toto nejake reakcie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#124 30. 08. 2012 17:04
Re: najkrajsia teorema
Dnes vam urobim radost z malym prazdninovym cvicenim.
Dokazte ze determinant danej stvorcovej matice typu 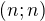 z koeficientamy v
z koeficientamy v 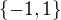 je nasobkom cisla
je nasobkom cisla 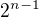
Podla mna dokaz nie je tazky, ale tento vyrok prekvapi viac ako jedneho.
Na riesenie pouzite skor toto vlakno:
http://forum.matweb.cz/viewtopic.php?pid=301347#p301347
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#125 12. 09. 2012 13:56
Re: najkrajsia teorema
Tu je zaujimave geometricke cvicenie
http://forum.matweb.cz/viewtopic.php?pid=302582#p302582
A podnych problemoch som uz vysie viac krat pisal...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

 ...
... pre miery vyjadrene v radianoch ).Tieto uhly su urcene danym zaroven ich sinusom a kosinusom , v orientovanej rovine.
pre miery vyjadrene v radianoch ).Tieto uhly su urcene danym zaroven ich sinusom a kosinusom , v orientovanej rovine.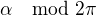 na
na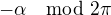
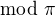 ( v radianoch)...cize budu urcene ich tangentom, pre danu orientaciu roviny. Zmena orientacie roviny, zmeny mieru
( v radianoch)...cize budu urcene ich tangentom, pre danu orientaciu roviny. Zmena orientacie roviny, zmeny mieru 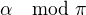 na
na 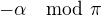
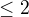 vdaka lubovolnym isometriam, tohto priestoru; ktory v tomto priapade nemusi byt orientovany, aby sme urcili ich mieru; ktora je v tomto pripade jednoznacne urcena na intevale
vdaka lubovolnym isometriam, tohto priestoru; ktory v tomto priapade nemusi byt orientovany, aby sme urcili ich mieru; ktora je v tomto pripade jednoznacne urcena na intevale ![kopírovat do textarea $[0; \pi]$](/mathtex/47/4797b9dac54b8b04eb4ac8382e87fa4c.gif) vdaka ich kosinusu
vdaka ich kosinusu a
a  su isometricke priamou isometriou; ako aj napriklad v priesrore dimenzii 3, vdaka rotacii uhla
su isometricke priamou isometriou; ako aj napriklad v priesrore dimenzii 3, vdaka rotacii uhla  ( ktorej restrikcia na rovinu (Oxy)je nepriama isometria ) okolo osy uhla
( ktorej restrikcia na rovinu (Oxy)je nepriama isometria ) okolo osy uhla  a
a 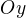 .
.