Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 11. 2018 22:15
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Janíčková posloupnost
Zdravím,
Narazil jsem zde: https://aeronet.cz/news/wp-content/uplo … nicko-.pdf
Jde perioda u obou posloupností nějak přepsat do geometrické řady s kvocientem 10?
Dík za názor
Offline
- (téma jako vyřešené označil(a) PlusPlusPlus)
#3 28. 11. 2018 01:27
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Janíčková posloupnost
Autor chybne pouziva pojem "suma cislic" misto pojmu ciferace / digital root: https://en.wikipedia.org/wiki/Digital_root Ten je roven zbytku po deleni deviti. Neni prekvapive, ze posloupnost zbytku Fibonaciho cisel po deleni deviti je periodicka: jakmile se jednou zopakuje dvojice zbytku, musi se opakovat i dalsi cleny. Vztah mezi obema posloupnostmi v clanku je take trivialni dusledek delitelnosti deviti. Delka periody fibonaciho cisel po deleni danym modulem je popsana v clanku https://en.wikipedia.org/wiki/Pisano_period
Doufam, ze je neco z vyse uvedeno relevantni k otazce -- nerozumim odkud se vzal kvocient 10.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 28. 11. 2018 15:29
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: Janíčková posloupnost
Ahoj,
Tak to je masakr. Naletěl jsem na příspěvek jednoho komentátora, přemýšlel jsem o tom nesmyslně asi takto: Periodu fibon.posloupnosti jsem hledal přes sumu:
Dál myšlení nebudu rozebírat, protože bych se musel stydět za moji slepotu. Hledal jsem tam víc, než v tom je. Zbytek po dělení 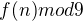 jsem si vůbec neuvědomil.
jsem si vůbec neuvědomil.
@Kondr - tak dík, pro mě dobrá lekce.
Offline
#5 28. 11. 2018 15:37
Re: Janíčková posloupnost
↑ PlusPlusPlus: Prve podozrenie by mal vyvolat server, kde je tato “vedecka praca” umiestnena ... aeronet :)
Offline
#6 28. 11. 2018 17:01
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: Janíčková posloupnost
↑↑ vlado_bb:
Zdravím a souhlasím. Téma uzavírám.
Offline
#7 28. 11. 2018 20:38 — Editoval PlusPlusPlus (28. 11. 2018 20:52)
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: Janíčková posloupnost
Jenom pro pořádek opravím původní myšlenkový řetězec:![kopírovat do textarea $
\sum_{k=1}^{\infty } \sum_{n=24k-23}^{24k} 10^{n-1} \left [ F_{n}-\left \lfloor \frac{F_{n}}{9} \right \rfloor9 \right ]=112358437189887641562819 \sum_{k=1}^{\infty } 10^{24k}
$](/mathtex/5e/5ea9bd10e4a47a85b7ceea4856aecec4.gif)
Myšlenku geometrické řady s kvocientem 10 jsem tam nakonec dostal.
Offline
#8 28. 11. 2018 21:02
Re: Janíčková posloupnost
Ono pojmenovat posloupnost po sobě chce taky jistou dávku narcismu. :D
↑ Kondr: včera tě vzpomněl Michal Bulant, když jsem se ho ptal na něco ohledně jeho semináře z algebry pro učitele :)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#9 28. 11. 2018 21:08
- PlusPlusPlus

- Příspěvky: 119
- Škola: SPŠS
- Pozice: brzy důchodce
- Reputace: 1
Re: Janíčková posloupnost
↑↑ byk7:
Zdravím. Možná narcismus, možná pohádka o Janíčkovi a Mařence... :D
Offline