Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 11. 2009 16:56 — Editoval PitBull~--! (20. 11. 2009 17:00)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
goniometrie
prosim jak se resi tenhle priklad: pocet vsech korenu rovnice sin6x=sin3x v intervalu <0,pi> je roven cislu... ?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#2 20. 11. 2009 17:16
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: goniometrie
Ze vzorce pro dvojnásobný argument rozepíšeme levou stranu jako 2sin(3x)cos(3x), rovnice má proto po úpravě tvar
sin(3x)(2cos(3x)-1)=0
Kdy je sin(3x)=0?
Kdy je cos(3x)=1/2?
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 20. 11. 2009 17:19
Re: goniometrie
↑ PitBull~--!:
Můžeš to odhadnout z grafu. Nebo vypočítat

 to ti dává 5 řešení v daném intervalu
to ti dává 5 řešení v daném intervalu
 to ti dává 2 řešení v daném intervalu
to ti dává 2 řešení v daném intervalu
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 20. 11. 2009 17:46
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: goniometrie
ale podle vysledku by to melo vyjit neco jinyho. Tady mam napsany, ze je to za e) a to je zadna z predchozich odpovedi neni spravna. za a)2 b)5 c)3 d)4
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#5 20. 11. 2009 17:52
Re: goniometrie
↑ PitBull~--!:
No samozřejmě, když je řešení 7. (2+5)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#6 20. 11. 2009 18:20
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: goniometrie
↑ zdenek1:
jee omlouvam se, nedaval sem se pozor
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#7 20. 11. 2009 18:54 — Editoval PitBull~--! (20. 11. 2009 18:55)
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: goniometrie
me to vyslo zase trochu jinak... u  sem vynasobil 2kou a vydelil sem to 9ti a vyslo mi x=pi/9+4kpi/9
sem vynasobil 2kou a vydelil sem to 9ti a vyslo mi x=pi/9+4kpi/9
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#8 20. 11. 2009 19:03
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: goniometrie
↑ PitBull~--!:
Původní perioda je kpí, ne 2kpí.
Offline
#9 20. 11. 2009 19:15
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: goniometrie
↑ halogan:
kpi je jenom u tangens a kotangens ne? tady je to dokonce i napsany http://cs.wikipedia.org/wiki/Goniometrick%C3%A1_rovnice
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#10 20. 11. 2009 23:01 — Editoval zdenek1 (20. 11. 2009 23:03)
Re: goniometrie
↑ PitBull~--!:
Nesmíš věřit všemu, co píšou na internetu. Nakresli si graf fce  a podívej se, s jakou periodou se opakuje nula.
a podívej se, s jakou periodou se opakuje nula.
Kosinus a sinus mají periodu  . Ale tohle je něco jiného, to není perioda funkce, ale perioda, se kterou se opakuje kořen této konkrétní rovnice.
. Ale tohle je něco jiného, to není perioda funkce, ale perioda, se kterou se opakuje kořen této konkrétní rovnice.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#12 20. 11. 2009 23:47
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: goniometrie
zkusil jsem to znovu spocitat a tentokrat mi vyslo u kosinusu k=4 (4reseni) a u sinusu u kpi k=1 a u pi+kpi k=0, takze mi to dohromady davalo 6 reseni. kde jsem zase udelal chybu?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#13 21. 11. 2009 02:15 — Editoval KennyMcCormick (21. 11. 2009 02:16)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: goniometrie
↑ PitBull~--!:
1.![kopírovat do textarea $sin6x=sin3x\wedge x\in[0;\pi]$](/mathtex/5d/5dd78cef185ec50f71e4dd2c8d70a873.gif)
2.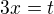
3.
4.
5.
6.
7.
8.
9.
10.
To jsou zatím 2 řešení. Protože jsem v pátém kroku udělal němý předpoklad a vyřadil případy, kdy  , připravil jsem se o několik řešení rovnice. Spočítám si, o kolik.
, připravil jsem se o několik řešení rovnice. Spočítám si, o kolik.




Další čtyři řešení navíc, už máme celkem 6 :)
Při přechodu z šestého řádku na sedmý je klíčové uvědomit si, že  . Proto dalším alternativním sedmým řádkem bude:
. Proto dalším alternativním sedmým řádkem bude:
7.
A dále:


Právě jsme získali sedmé řešení.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#14 21. 11. 2009 10:48
- PitBull~--!

- Příspěvky: 208
- Reputace: 0
Re: goniometrie
↑ zdenek1:
ja jsem tomu rozumel tak, ze kdyz je to jenom pul kruh <0,pi>, tak u sinusu a cosinusu bude misto 2kpi jenom kpi a u tangens a cotangens bude kpi/2?
___ ̴̡ı̴̡̡ *̡͌l̡*̡̡_*̡͌l̡*̡̡ ̴̡ı̴̴̡__ ̡̡͡|̲̲̲͡͡͡ ̲▫̲͡ ̲̲̲͡͡π̲̲͡͡ ̲̲͡▫̲̲͡͡ ̲|̡̡̡ ̡ ̴̡ı̴̡̡ *̡͌l̡*̡̡___
Offline
#16 21. 11. 2009 11:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometrie
↑ halogan:
Nostalgie a pravidla...
Taková znění zadání jsou v přijímacích testech na VŠE (určitě si to pamatujeme :-) Kolega halogan vysvětloval pomocí univerzální teorienávod, jak se má číst zadání a jak se má použit výsledek k volbě spravné odpovědí.
Chce se někomu udělat (nebo vyhledat? - máme toho hodně, ale ne všechno je vzorové) další vzorová řešení?
----
Ke konkrétnímu zadání -
halogan napsal(a):
Zopakuj si teorii.
Souhlas, neboť tato úloha se nejlépe řeší pomocí grafu goniometrické funkce - naznačuje i kolega Zdeněk1 (neboť se nikdo neptá na hodnoty kořenů, ale na jejich počet v intervalu). Doufám, že nenarušuji kvalitní výklad - už odcházím na tradiční cestu Opavou (ovšem dnes v práci budu mít velký časový prostor, neb tam budu celý vikend hlavně přebírat výsledky práce našeho programátora, ale hlavně zajišťovat, aby netrpel hlady a neklesal na myslí). Tak se snad konečně připojim k debatě o pravidlech. Pozdrav :-)
Offline