Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spektrální rozklad matice (TOTO TÉMA JE VYŘEŠENÉ)
#78 22. 12. 2009 15:51
#81 26. 12. 2009 17:46
Re: Spektrální rozklad matice
Dobrý den,
Vím že to zde již zaznělo ale potřeboval bych spočítat spektrální rozklad matice
1 -1 0
-1 1 1
0 1 1
Nepotřebuji to spočítat celé jen potřebuji přijít na to jak vytvořit rovnici ze které následně zjistím vlastní čísla matice. Díval jsem se snad všude ale nemůžu na to přijít pokaždé mi to vyjde špatně.
Offline
#82 26. 12. 2009 21:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ Nedvd:
Zdravím,
teorie zazněla ihned v 2. příspěvku, konkrétně tvé zadání - v příspěvku 64 v tomto tématu, ve shodě se strojem (klepnout na exact <-> approximate form) + místní archiv.
Napíš, co konkrétně vychází špatně a také doporučuji nový dotaz do samostatného tématu.
....
Offline
#83 26. 12. 2009 23:29
Re: Spektrální rozklad matice
Jedná se o to že pokud mám takto zadanou matici tak nevím jak z ní vytvořit rovnici kvadratickou. Vyjde mi vždy nějáký chybný výraz. Potřeboval bych to přesně rozepsat do závorek se stručným komentářem co s čím se násobí a proč (zda-li jsou tam pravidla). Ná stránkách cvičícího jsem to nenašel. Měl to tam uvedeno jen v definicích přes 3 řádky které jsou pro mě španělská vesnice
Offline
#84 26. 12. 2009 23:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ Nedvd:
Toto je srozumitelne? http://forum.matweb.cz/viewtopic.php?pid=63267#p63267 - to je ovšem matice na 4. řádky, snad najdu i na 3.
Offline
#86 26. 12. 2009 23:50
Re: Spektrální rozklad matice
Vím že rovnice bude kubická uvedl jsem to jen jako pojem pro popis problému. Ovšem stále jsem nepochopil na jakém principu se to roznásobuje. Tu první část jsem ještě pochopil ale ta druhá jak lze poskládat tu druhou část myslím tím -1 *|....|.
Offline
#87 26. 12. 2009 23:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ Nedvd:
došla a našla - je to na principu výpočtu determinantu (to také není v materiálech?)
Offline
#88 27. 12. 2009 00:00
Re: Spektrální rozklad matice
Všechny příspěvky jsem si zde právě prošel ovšem nepochopil jsem z toho jak dojít k té rovnici pro výpočet tohoto. Věděla bys jaká je rovnice u té mojí matice? Pokud ano zkus ji napsat zkusít to z toho pochopit já vždycky došel k rovnici
|1-x 1 | |-1 1-x |
(1-x) |1 1-x | + (-1) | 0 1 | Vím že tohle je špatně ale nevím proč
Offline
#89 27. 12. 2009 00:10
Re: Spektrální rozklad matice
↑ Nedvd:
Protože neumíš použít větu o rozvoji determinantu podle řádku/sloupce. Ta říká, že determinant matice se dá vyjádřit jako jakási suma, kde každý sčítanec obsahuje součin určitého prvku té matice a subdeterminantu matice, který z té původní matice vznikne, když se z ní vypustí ten řádek a sloupec, ve kterých ten prvek je. Navíc je každý sčítanec opatřen nějakým znaménkem, podle pozice toho prvku v původní matici. Detaily snadno najdeš někde tady ve fóru nebo na internetu. A taky to je určitě je v těch materiálech na stránkách cvičícího, které jsou patrně pod tvou úroveň - což je chyba.
Říká se tomu "věta o rozvoji determinantu podle sloupce", "Laplaceův rozvoj determinantu", "Laplaceova věta" a podobně.
Offline
#90 27. 12. 2009 00:20 — Editoval jelena (27. 12. 2009 01:58)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ Nedvd:
po doplnění "lambd" (ve tvém případě máš označení "x") shodně rozkládáme dle 1. řádku:
Do hranatých závorek jsem dala jednotlivé subdeterminanty.
Z náhledu vidím, že kolega Lukáš )pozdrav :-) již všechno vysvětlil, ale když už jsem si dala takovou práci, tak to zde zanechám (termín u ostravských informatiků je myslím 09.01. - určitě ještě bude potřeba).
EDIT: abych v tom měla systém - je to zadání 19, komplet teorie od pana Vondráka obsahuje všechno, co je potřeba.
Offline
#91 27. 12. 2009 18:46 — Editoval lantian (27. 12. 2009 19:41)
Re: Spektrální rozklad matice
Zdravím,
prosím o pomoc při řešení spektrálního rozkladu této matice :
Nevím jestli se jedná o nějaký speciální typ nebo někde dělám chybu, ale nemohu se dopočítat vlastních čísel a vektorů.Podle wolfram alpha by to mělo být následovně: (viz Odkaz )
speciálně se nemohu dopočítat vlastního vektoru pro číslo 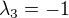 , takže buď neumím řešit tuto soustavu nebo je něco špatně :-P
, takže buď neumím řešit tuto soustavu nebo je něco špatně :-P
Vychází mi to jako nulový vektor, což je špatně.
Předem díky za pomoc nebo tip..
Offline
#92 27. 12. 2009 20:00 — Editoval jelena (27. 12. 2009 20:06)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ lantian:
celé jsem to nekontrolovala, ale v posledni matici na pozicích, co máš nuly, má být 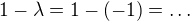 pomůže?
pomůže?
EDIT: vychází na 2 parametry, tedy může vyhovovat vektor (1, 1, 1), co navrhuje stroj.
Offline
#94 27. 12. 2009 20:37
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Spektrální rozklad matice
↑ lantian:
skalární součin v_1, v_2 činí problém asi? Pro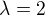 také vychází na 2 parametry a pokud se podaří vybrat vhodně, tak je vyřešeno. A jelikož kolegovi se podařilo vybrat vhodně, tak přeber jeho vektory: http://forum.matweb.cz/viewtopic.php?id=1098 - tvému zadání to vyhovuje (dle mé rychlé kontroly), ale překontroluj ještě, prosím.
také vychází na 2 parametry a pokud se podaří vybrat vhodně, tak je vyřešeno. A jelikož kolegovi se podařilo vybrat vhodně, tak přeber jeho vektory: http://forum.matweb.cz/viewtopic.php?id=1098 - tvému zadání to vyhovuje (dle mé rychlé kontroly), ale překontroluj ještě, prosím.
Offline
#95 04. 01. 2010 22:52
Re: Spektrální rozklad matice
Zdravím. Potřeboval bych zkontrolovat tento spektrální rozklad. 
Když provedu zkoušku (Ut*D*U) tak mi matice A nevyjde.
Vlastní čísla a vektory jsem si kontroloval pomocí Wolframu, a napadlo mě jestli nevadí pořadí ve kterém jsem použil vl. čísla a pak i vektory. Wolfram mi je dal v jiném pořadí, takže i ty matice U a D pak budou vypadat jinak, což ovlivní i výsledek zkoušky. Děkuji za odpověď.
Offline
#96 04. 01. 2010 23:08 — Editoval LukasM (04. 01. 2010 23:08)
Re: Spektrální rozklad matice
↑ Rhodry:
Ahoj. Mám pocit, že jsi přehodil matice U a UT.
Jinak je tu dobrým zvykem zakládat pro nový dotaz nové téma. Pak v tom není takový bordel. Je na to upozorňováno na spoustě míst, mimo jiné v pravidlech a potom u vyřešených témat hned u tlačítka ODESLAT, když se posílá nový příspěvek - ale evidentně to stále nestačí ;-)
Offline
#97 05. 01. 2010 10:43
Re: Spektrální rozklad matice
Děkuji, opravdu v tom byla chyba. Ze svojich materiálů jsem pochopil že vl. vektory se dávají do sloupců matice U, i když to má být do řádků.
Jinak zakládat nové téma kvůli mému dotazu mi přišlo zbytečné, a toho upozornění že je téma vyřešeno jsem si všim, avšak v tomhle případě jsem se jej rozhodl ignorovat :) Asi to je síla zvyku z jiných míst, kde nechcou zbytečně nové témata když už se to někde řeší nebo řešilo ;)
Offline
#98 05. 01. 2010 11:00 — Editoval LukasM (05. 01. 2010 11:01)
Re: Spektrální rozklad matice
↑ Rhodry:
Jo, však v pohodě, já jsem to nijak zle nemyslel. Já to znám taky, třeba z cyklodiskuze.cz. Tady je to ale trochu něco jiného, každý příklad je přece jen jiný, a každý dělá jiné chyby, takže riziko že tu bude někdo psát něco pořád dokola tu není takové. Samozřejmě se tu dá hledat a něco se naučit z chyb ostatních, ale když už nic nenajdeš a chceš se zeptat, tak se neboj založit nové téma (pokud to opravdu přímo nenavazuje na nějaké existující - jako dotazy typu "jak jsi udělal tohle a tohle?"). Měj se.
Edit: Ty jo, já tady prudim s pravidlama, přitom jsem právě napsal OT do uzavřeného tématu :-)
Offline
#100 05. 01. 2010 18:28
Re: Spektrální rozklad matice
↑ Rygy:
Ahoj. Máš to dobře, takže si to třeba roznásob a posčítej co půjde. Dostaneš rovnici třetího stupně, kterou rozložíš na součin - nejlépe asi tzv. metodou "hádání kořenů", a dostaneš tak vlastní čísla matice.
Každopádně to šlo dělat o něco šikovněji. Ty ses k tomu výrazu dostal patrně aplikací Sarrusova pravidla, což už tak obnášelo dost počítání, a teď to budeš ještě roznásobovat a ke všemu hádat kořeny. Kdybys na začátku přičetl poslední sloupec k prvnímu a potom od posledního řádku odečetl první, stačilo by determinant rozvinout podle posledního řádku a získání vl. čísel by obnášelo vyřešení jediné kvadratické rovnice, počítání by tam nebylo moc, a nebylo by třeba nic hádat.
Nic o zakládání nových témat tu už dneska radši psát nebudu, nemá to cenu. Jenom poznamenám, že než se na něco zeptáš, dá se trochu hledat na fóru a najít inspiraci. Nevím co mi říká žes to neudělal - k tvému pobavení doporučuji příspěvky v tomto vlákně ze včerejšího večera/dnešního dopoledne.
Offline
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Spektrální rozklad matice (TOTO TÉMA JE VYŘEŠENÉ)

 ?
?