Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Ostatní
- » смесь математики для любителей русского n (TOTO TÉMA JE VYŘEŠENÉ)
#26 01. 07. 2008 22:31 — Editoval jelena (07. 06. 2014 00:11)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
Jen se bavim :-)
замена 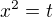
 , отсюда
, отсюда 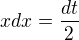

вернем замену
еще производная
http://uloz.to/540815/derivace-5.pdf
http://www.youtube.com/watch?v=i4l2ZJF1R38
http://www.youtube.com/watch?v=5nVoq0FZ2OA
Offline
#28 02. 07. 2008 00:09 — Editoval jelena (14. 06. 2009 01:02)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
↑ ttopi:
Добрый вечер, милый друг Ттопи :-)
как умею, так и развлекаюсь :-) - а серьезно - это было для друзей здесь :-)
Опять развлекаюсь - на этот раз для Дагмар
Benzen C6H6 se hydrogenuje za vzniku cyklohexanu C6H12. určete rovnovážnou konstantu reakce Kc, jestliže výchozí koncentrace benzenu je 3 mol/l, vodíku 8 mol/l a do ustanovení rovnováhy je zreagováno 70% benzenu.
Reakce: 
![kopírovat do textarea $K_c=\frac{[ C_6H_{12}]}{[ C_6H_{6}][ H_{2}]^3} $](/mathtex/fa/fa0779f478dcebb63301fb118dde32e7.gif)
1 mol benzenu reaguje teoreticky s 3*1 mol vodiku, benzen je v nedostatku, vypocet je veden podle benzenu.
Reagovalo 70 % benzenu 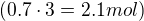 , to znamená, že vzniklo stejné množství cyklohexanu (2,1 mol) – to je na straně produktů.
, to znamená, že vzniklo stejné množství cyklohexanu (2,1 mol) – to je na straně produktů.
Na straně reaktantů zůstalo 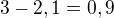 mol benzenu a
mol benzenu a  mol vodíku. Dosazujeme do vzorce pro rovnovažnou konstantu:
mol vodíku. Dosazujeme do vzorce pro rovnovažnou konstantu:![kopírovat do textarea $K_c=\frac{[ 2,1]}{[ 0,9][1,7]^3}= 0,47$](/mathtex/04/04cb05a48b998f5a9f3c2a7b1041b122.gif)
====================================
2. Určete disociační stupeň a pH slabé jednosytné zásady o koncentraci c= 0,05 mol*dm -3, jejíž disociační konstanta 

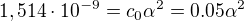 , odsud
, odsud 
pro slabé zásady ![kopírovat do textarea $pH=14-\frac12(pK_B-\log[BOH])$](/mathtex/32/32b2a8c1584f4aa76b35c5e4e23ce0ce.gif) , kde
, kde 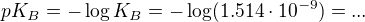
pro slabé kyseliny ![kopírovat do textarea $pH=\frac12(pK_A-\log[HA])$](/mathtex/ad/ad4d9b3b67decd277ec1fc33fcf3d8b4.gif) , kde
, kde 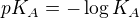
Offline
#29 01. 08. 2008 11:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
Ишь ты! -- ответил Незнайка. -- А я и не знал, что солнце такое большое. Пойду-ка расскажу нашим -- может быть, они еще не слыхали про это. А ты все-таки посмотри на солнце в свою трубу: вдруг оно на самом деле щербатое! Незнайка пошел домой и всем, кто по дороге встречался, рассказывал: -- Братцы, вы знаете, какое солнце? Оно больше всей нашей Земли. Вот оно какое!
Привет от Незнайки :-)
Offline
#30 17. 08. 2008 09:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
Zdravím vás :-)
Přidám odkaz na možnost psaní ruských textů bez ruské klávesnice: www.translit.ru nebo http://ge.translit.cc/ - je možnost také psaní řeckých písmen (to možná využijete více :-) a dalších řečí.
Napsaný text je potřeba zkopírovat a vložit do zprávy.
Hodně zdaru :-)
Offline
#32 17. 08. 2008 09:54 — Editoval jelena (28. 09. 2009 10:08)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
↑ ttopi:
почему плохо? - правильно написано :-)
Ja jsem na tuto možnost přišla na ruské elektronické knihovně www.aldebaran.ru - oni tam jsou děsně citlivé na psaní latinkou na forum nebo do knihy návštěv (tedy pokud někdo piše rusky latinkou) a proto pořad doporučuji používat nějaké pomůcky.
Byla to taková dobrá elektronická knihovna, ale teď, než se človek dokope k nějaké knižce, tak leze kde jaká reklama, navíc s obsahem ...... Tak si alespoň přečtu názory a polemiku o knižkách a musím se podívt jinam (stejně nakonec zůstavám u klasiky, co mám v papírové podobě, před pořízením e-booku nějak váhám.
Zdravím :-)
Planimetrie pro gymnázia:
2.19 a) |AB|= =6 cm,
=6 cm,  =5 cm,
=5 cm,  =5 cm (zadání: strana, těžnice na stranu, strana) Odkaz
=5 cm (zadání: strana, těžnice na stranu, strana) Odkaz
2.19 d)  ,
,  ,
,  (zadání: strana, výška na stranu, protilehlá úhel) Odkaz
(zadání: strana, výška na stranu, protilehlá úhel) Odkaz
2.20 b)  =60°,
=60°,  =5,5cm
=5,5cm  =|BC|=6 cm (zadání: úhel, těžnice, strana) Odkaz (nehotovo)
=|BC|=6 cm (zadání: úhel, těžnice, strana) Odkaz (nehotovo)
2.20 b) BC= =5 cm,
=5 cm,  = 5.5 cm a uhel
= 5.5 cm a uhel  = 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz
= 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz
2.20 c) BC= =5cm,
=5cm,  =3 cm,
=3 cm,  =5 cm (zadání: strana, výška na stranu, těžnice na jinou stranu) Odkaz
=5 cm (zadání: strana, výška na stranu, těžnice na jinou stranu) Odkaz
2.20 b) BC= =5 cm,
=5 cm,  = 5.5 cm a uhel
= 5.5 cm a uhel  = 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz
= 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz
2.21 a)  =4 cm,
=4 cm,  =5cm,
=5cm,  =5 cm (zadání: strana, výška na jinou stranu, těžnice na další stranu) (nehotovo) Odkaz
=5 cm (zadání: strana, výška na jinou stranu, těžnice na další stranu) (nehotovo) Odkaz
2.21 c) je dána úsečka |AA_0|= =4 cm, sestrojte všechny trojúhelníky ABC pro které platí
=4 cm, sestrojte všechny trojúhelníky ABC pro které platí  =6 cm,
=6 cm,  = 2,5 cm (strana, dvě výšky na zbývající strany)
= 2,5 cm (strana, dvě výšky na zbývající strany)
2.22 b) Je dána úsečka |AA_1|= =6 cm, sestrojte všechny trojúhelníky ABC, pro které platí
=6 cm, sestrojte všechny trojúhelníky ABC, pro které platí  =8 cm,
=8 cm,  = 5 cm (zadání: strana, těžnice na stranu, výška na stranu) Odkaz
= 5 cm (zadání: strana, těžnice na stranu, výška na stranu) Odkaz
(není kompletní, pouze 1. zadání)
2.22 c) je dána úsečka |AA_1| = = 6 cm, sestrojte všechny trojúhelníky ABC, pro které platí úhel
= 6 cm, sestrojte všechny trojúhelníky ABC, pro které platí úhel  =60°;
=60°;  = 4,5 cm (zadání: dvě těžnice, úhel) Odkaz
= 4,5 cm (zadání: dvě těžnice, úhel) Odkaz
2.22 c) je dána úsečka AS, |AS|= =5 cm. Sestrojte všechny trojúhelníky ABC s těžnicí AS, pro které platí: těžnice
=5 cm. Sestrojte všechny trojúhelníky ABC s těžnicí AS, pro které platí: těžnice  = 8 cm, úhel
= 8 cm, úhel  = 30° (těžnice na stranu a, těžnice na stranu b, úhel) Odkaz
= 30° (těžnice na stranu a, těžnice na stranu b, úhel) Odkaz
(překontrolovat).
2.22 c)  ,
,  ,
,  (zadání : dvě těžnice, úhel) Odkaz
(zadání : dvě těžnice, úhel) Odkaz
2.24)  =75,
=75,  =3,5 cm,
=3,5 cm,  =2,5 cm (zadání: úhel, výška na protilehlou stranu, poloměr opsané kružnice) Odkaz, Odkaz, Odkaz, Odkaz
=2,5 cm (zadání: úhel, výška na protilehlou stranu, poloměr opsané kružnice) Odkaz, Odkaz, Odkaz, Odkaz
2.25 – jiné označení)  ,
,  ,
,  - poloměr kružnice vepsané (úhel, protiléhlá strana, poloměr kružnice vepsané) Odkaz
- poloměr kružnice vepsané (úhel, protiléhlá strana, poloměr kružnice vepsané) Odkaz
(překontrolovat)
2.25) úhel  = 45,
= 45,  =5 cm,
=5 cm,  poloměr kružnice vepsané (1,5cm) (zadání: úhel, protiléhlá strana, poloměr r kužnice vepsané) Odkaz, Odkaz, Odkaz
poloměr kružnice vepsané (1,5cm) (zadání: úhel, protiléhlá strana, poloměr r kužnice vepsané) Odkaz, Odkaz, Odkaz
2.28) pravoúhlý trojúhelník ABC s pravým vrcholem u C, a=4,5 cm a  poloměr vepsané kružnice=1,5 cm (pravoúhlý trojuhelník, odvěsná, poloměr vepsané kružnice) Odkaz Odkaz
poloměr vepsané kružnice=1,5 cm (pravoúhlý trojuhelník, odvěsná, poloměr vepsané kružnice) Odkaz Odkaz
3.15) sestrojit trojúhelník, dáno:  =4 cm, úhel
=4 cm, úhel  = 60°,
= 60°, 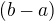 =1 cm (zadání: strana, přílehlý úhel, rozdíl stran, návod – osová souměrnost, symetrie) Odkaz
=1 cm (zadání: strana, přílehlý úhel, rozdíl stran, návod – osová souměrnost, symetrie) Odkaz
3.15)  ,
,  ,
,  (zadání: rozdíl stran, třetí strana, přílehlý úhel, návod: osová souměrnost, symetrie). Odkaz, Odkaz
(zadání: rozdíl stran, třetí strana, přílehlý úhel, návod: osová souměrnost, symetrie). Odkaz, Odkaz
3.16 b) Sestrojte  ABCD, je-li dáno
ABCD, je-li dáno  =7 cm,
=7 cm, 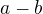 =1 cm (zadání: ondélník, rozdíl stran, uhlopříčka, návod: osová souměrnost) Odkaz
=1 cm (zadání: ondélník, rozdíl stran, uhlopříčka, návod: osová souměrnost) Odkaz
3.17) sestrojit  ABCD, dáno:
ABCD, dáno:  = 5 cm,
= 5 cm,  = 5.5 cm
= 5.5 cm  = 6 cm (přímka AC je osou souměrností deltoidu) (zadání: strana, úhlopříčky, deltoid, návod: osová souměrnost, symetrie). Odkaz
= 6 cm (přímka AC je osou souměrností deltoidu) (zadání: strana, úhlopříčky, deltoid, návod: osová souměrnost, symetrie). Odkaz 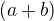 =10 cm,
=10 cm,  =6,2 cm,
=6,2 cm,  70 stupňů (zadání: strana, protilehlý úhel, součet stran (zbývajících), zdroj:- , návod: osová souměrnost, symetrie). Odkaz
70 stupňů (zadání: strana, protilehlý úhel, součet stran (zbývajících), zdroj:- , návod: osová souměrnost, symetrie). Odkaz
Odkaz
3.15 a) 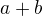 =10,
=10,  =5,
=5,  =3 (zadání: strana, součet stran (zbyvajících), výška, další zdroj: Petáková, kap. 10.6, úloha 49 a), Odkaz
=3 (zadání: strana, součet stran (zbyvajících), výška, další zdroj: Petáková, kap. 10.6, úloha 49 a), Odkaz
poloměr kružnice vepsané a velikost přepony v pravoúhlém trojúhelníku (4 řešení)
Odkaz
(nehotovo)
3.86 b)  = 5 cm,
= 5 cm,  = 2:3:4 (zadání: výška, poměr všech stran, další zdroj: Petáková, kapitola 10.9, úloha 72 e), návod: stejnolehlost)
= 2:3:4 (zadání: výška, poměr všech stran, další zdroj: Petáková, kapitola 10.9, úloha 72 e), návod: stejnolehlost)
Odkaz
Petáková:
kap. 10.4, ulohy 14 až 17 (je potřeba probrat :-) Odkaz Zadání, Řešení
kap. 10.4, úloha 18 a) použito jiné označení)  =6.5 cm,
=6.5 cm,  =60°,
=60°,  =|BC|=6 cm (zadání: strana, strana, protilehlý úhel) Odkaz
=|BC|=6 cm (zadání: strana, strana, protilehlý úhel) Odkaz
kap. 10.4 úloha 18 e) , použito jiné otnačení)  ,
,  ,
,  (zadání: strana, 2 těžnice na další strany) Odkaz
(zadání: strana, 2 těžnice na další strany) Odkaz
kap. 10.4, úloha 18 f) použito jiné označení ) Trojúhelník KLM:  =5 cm,
=5 cm,  =9 cm,
=9 cm, 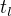 =6 cm (strana, dvě tečny) Odkaz
=6 cm (strana, dvě tečny) Odkaz
kap. 10.4, úloha 18 m)  =9 cm,
=9 cm,  =7,5 cm,
=7,5 cm,  =6,5 cm (strana, těžnice na stranu, výška na jinou stranu) Odkaz
=6,5 cm (strana, těžnice na stranu, výška na jinou stranu) Odkaz
kap. 10.4, úloha 18 n)  =6 cm,
=6 cm,  =5 cm
=5 cm  =4,5 cm (strana, výška na stranu, výška) Odkaz
=4,5 cm (strana, výška na stranu, výška) Odkaz
kap. 10.4, úloha 18q)  ,
,  , úhel
, úhel  (zadání: strana, výška na stranu, protilehlý úhel, zdroj: Petáková, Odkaz
(zadání: strana, výška na stranu, protilehlý úhel, zdroj: Petáková, Odkaz
kap. 10.4, úloha 18 r)  = 4 cm,
= 4 cm,  = 3 cm a
= 3 cm a  : a) 60 stupnu b) 120 stupnu (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
: a) 60 stupnu b) 120 stupnu (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
kap. 10.4, úloha 18 r)  ,
,  , úhel
, úhel  (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
(zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
kap. 10.4, úloha 18 r)  =4 cm ,
=4 cm ,  =3 cm, úhel
=3 cm, úhel  =60˚ (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
=60˚ (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
kap. 10.4, úloha 18 r)  ,
,  ,
,  (zadání: strana, protilehlý úhel, těžnice na jinou stranu, návod: středová souměrnost) Odkaz
(zadání: strana, protilehlý úhel, těžnice na jinou stranu, návod: středová souměrnost) Odkaz
kap. 10.4, úloha 18 s)  ,
,  , úhel
, úhel  Odkaz
Odkaz
kap. 10.4, úloha 18 u) =4 cm,
=4 cm,  =45,
=45,  = 60 (těžnice na stranu a úhly straně přilehlé), Řešení
= 60 (těžnice na stranu a úhly straně přilehlé), Řešení
kap. 10.4, úloha 20 a)  ,
,  ,
,  - poloměr kružnice vepsané (zadání: strana, přilehlý úhel, poloměr kružnice vepsané) Odkaz
- poloměr kružnice vepsané (zadání: strana, přilehlý úhel, poloměr kružnice vepsané) Odkaz
kap. 10.4, úloha 20 b) =4 cm,
=4 cm,  =60 stupnu,
=60 stupnu,  =1,5 cm (polomer kruz. vpisanej) (zadání: výska na stranu, úhel, poloměr kružnice vepsané Odkaz
=1,5 cm (polomer kruz. vpisanej) (zadání: výska na stranu, úhel, poloměr kružnice vepsané Odkaz
kap. 10.4, úloha 23 c) Zostrojit  , ak pozname dlzku jeho stran (
, ak pozname dlzku jeho stran ( ,
,  ,
,  ,
,  )? (lichoběžník, délka všech stran) Odkaz
)? (lichoběžník, délka všech stran) Odkaz
kap. 10.6, úloha 49 d) obvod  =12cm,
=12cm,  =3cm, úhel
=3cm, úhel  60° (obvod trojúhelníku, výška, úhel) Odkaz
60° (obvod trojúhelníku, výška, úhel) Odkaz
kap. 10.9, úloha 72 e),  = 5 cm,
= 5 cm,  = 2:3:4 (zadání: výška, poměr všech stran, Zdroj: Planimetrie pro gymnázia, úloha 3.86 b), Petáková, návod: stejnolehlost)
= 2:3:4 (zadání: výška, poměr všech stran, Zdroj: Planimetrie pro gymnázia, úloha 3.86 b), Petáková, návod: stejnolehlost)
Odkaz
kap. 10.9, úloha 72 g) poměr stran  = 5:6:5,
= 5:6:5,  (poloměr kružnice vepsané) je 2 cm Odkaz
(poloměr kružnice vepsané) je 2 cm Odkaz
Offline
#34 17. 08. 2008 10:12 — Editoval jelena (05. 03. 2009 17:39)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
↑ ttopi:
:-) na translit.ru překladač je dole vyznačiš text, dole zvoliš slovník a pak klep "перевести текст"
Why it is bad? - it is correctly written
Por qué malo? - es correctamente escrito
Ale Deutsch to nějak nechytá Warum плохо? - ist richtig geschrieben
Nic, musím jit luxovat (пылесосить - nebolí /odsavat prach :-)
http://newstar.rinet.ru/~goga/biblio/lipson/lipson.djvu
Offline
#35 28. 09. 2008 13:22 — Editoval jelena (13. 06. 2009 00:31)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
Zdravím vás :-)
Aby to nevypadalo, že ruské téma je zanedbáné, přidám, co v poslední době velmi pobavilo: „polopatický výklad „Smrtonosná past 1 až 3“
Dobré hlášky :-) „Но если Джон жив, то надежда осталась", "Он победит злодеев, даже лысый и босой"
A něco užitečného do zeměpisu a do teorie grafu (souvislost s ruskou strankou to má chabou - odkaz na mapu jsem dostala od snámych z Východu :-)
Так, пойду гулять по Опаве по направлению "работа". Погода у нас прекрасная, привет вам :-)
Offline
#36 01. 09. 2009 12:02
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
Zdravim vás,
abych nenarušovala zdarný návrat k problemu exaktních rovnic, za poslední příspěvek děkuji :-) a také jelikož mám dovolenou za účelem užitečných okruhů Opavou - пойду гулять (ZŠ, ŠJ - hotovo, ještě ZUŠ 1, ZUŠ 2), využiji času a přidám odkaz na online radio:
není to příliš kvalitní, trochu ruší reklama, ale zas není nutné řešit stahování a uspořádání - stačí zvolit již hotový výběr: například: 461 skladeb Vysockého. Je potřeba pod "růžovým oknem" klik na Слушать или Перемешать а Слушать. Nekteré skladby jsou opakovaně, v různém provedení, u některých skladeb je doplněn i text.
Až se obnoví činnost tohoto webu, tak to byla nejlepší možnost kompletního poslechu černých desek ve slušné kvalitě a bez reklam, snad to bude i po obnově (měli tam nejlepší sbírku skladeb Vysockého).
----------------------------------
Tvorba Vysockého a jeho osobnost je příliš vážné téma, bojim se, abych o něm nemluvila nějak povrchně. Asi ani není nutné, abych sdělila, že můj vztah není jen v rovině "libí", ale je projevem velké úcty. Také jsem měla za to, že Vysocký je obtížně přeložitelný a pochopitelný, jelikož je obtížně přenositelný jak generačně, tak i místně (například, když бермуторно на сердце и бермудно на душе).
A jsem moc potěšena, že snad není tomu tak - doposud jsem zde umístila jednu skladbu a jeden výtah z textu, jelikož mi přišlo snadnější umísťovat něco méně zodpovědného a nenáročného. Tak uvidím, zda tuto svoji obavu překonám.
A pokud bych měla zvolit frazi, kterou používám, tak to je například "Еще не вечер" (omlouvám se za obrazovou stranku, ale hledala jsem verzi bez orchestralního doprovodu).
Pokud byste měli zájem o volný překlad nebo upřesnění některého textu, jsem k službam a budu se těšit.
Ještě upozorním na velmi vtipnou anglicko - ruskou učebnici, lekce 1 od str. 18 djvu - užijte si a hodně zdaru:-)
Offline
#37 06. 09. 2009 15:45
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: смесь математики для любителей русского n
Zdravím a děkuji za odkazy, i ta učebnice je celkem zajímavá :) Aspoň víme, co dělají úderníci v parku :)
Offline
#38 20. 11. 2009 13:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
↑ kaja(z_hajovny):
Narazila jsem na velmi roztomilou úlohu z pravděpodobnosti - znaté k tomu odpovídající písen našeho oblibeného barda?
Mějte se hezky :-)
Offline
#39 11. 12. 2009 23:43 — Editoval jelena (11. 12. 2009 23:44)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
Slibila jsem kolegovi Zdeňkovi, že doplnim materiály ohledně přijímacích zkoušek matematiky v Rusku.
Začátek povídání byl zde, skutečně je to tak, že většina škol přešla na akceptování výsledku Jednotné státní zkoušky (ЕГЭ), zkouška ovšem má základní a speciální úroveň. Školy, co mají zkoušky, jsou zejména MGU (Lomonosovova univerzita), FIZTECH, MIFI - také maji vlastní systém přípravy a olympiad.
Z technik:
- obdoba ČVUT: http://fn.bmstu.ru/math/abitur/parshev/ … index.html
- energetická VŠ http://www.mpei.ru/lang/rus/entrants/co … amples.asp
- technika S_Peterburg http://www.mathnet.spb.ru/univexams.htm nebo http://www.mathnet.spb.ru/texts/ffexam/fftext.pdf
http://www.edu.ru/moodle/ (vstupuje se jako host)
Nejvíce materiálů ke stažení je zde (za reklamy se omlouvám):
http://www.alleng.ru/edu/math.htm výběr pro přípravu ke zkouškám (byla u nás na návštěvě kamarádka se synem a ten pořád měl takové knihy :-)
http://www.alleng.ru/d/math/math382.htm
http://www.alleng.ru/d/math/math270.htm
http://www.alleng.ru/d/math/math38.htm
http://www.alleng.ru/edu/math5.htm
http://dwl.alleng.ru/d_ar/math/math25.zip - to se mi libilo, úlohy s parametry, těch není moc, pěkná sbírka.
I nadale je aktuální standardizovaná sbírka, na kterou se odkazuji zde
Pokud bude něco potřeba doplnit nebo lehce přeložit, jsem k službam :-)
Offline
#41 04. 03. 2010 11:23
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: смесь математики для любителей русского n
↑ Josef Palat:
Toto není vhodné místo pro umístění tohoto dotazu. Založ si vlastní téma v příslušné sekci, pak to tu smažu.
Offline
#42 05. 03. 2010 09:37
- Josef Palat
- Zelenáč
- Příspěvky: 11
- Reputace: 0
Re: смесь математики для любителей русского n
↑ BrozekP:nevím kde a jak pro dotaz založit sekci poradte dík
Offline
#43 05. 03. 2010 11:44
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: смесь математики для любителей русского n
Na úvodní stránce klikneš postupně na odkazy "Vysoká škola" a "založit nové téma", dostaneš se sem.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#44 05. 03. 2010 11:46 — Editoval jelena (05. 03. 2010 14:15)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: смесь математики для любителей русского n
↑ Josef Palat:
Zdravím,
téma si založiš ve stejné sekci Ostatní nebo ve Střední škola - nahoře je nápis Založit nové téma.
Pokud je to výpočtová úloha, tak určitě se dostane nápovědy k řešení (pokud to je ovšem něco praktického, tak spíš nějaké odborné fórum. I když nepochybuji, že tady se najde řada odborníků na různé zcela nečekané obory.
Co jsem si vybavila ze zadání, tak početně bych si zakreslila 1. azimut a délku 11,5 cm (úměrně době, po kterou plaveš, předpokládám stejnou rychlost), pak další azimut a opět délku 9,5 cm.
Toto není dobrý výpočet: Kreslila jsem bez délek, pouze pro úhly (azimut je od svislého směru na sever ve směru hodinových ručíček) a můj výsledek pro poslední azimut je 180 stupňů. Použivala jsem dvojice úhlu a dopočty do 180 stupňů v trojuhelníku a do 360 stupňů pro azimuty. Ale bylo to jen tak narychlo, proto bez záruky.
EDIT: s použitím zadaných délek a azimutů se použije cosinova věta pro dopočet zbývajících hodnot.
-----
V tomto tématu je stejně takový кошмарный бардак, že nějaký azimut mu stejně nemůže ubližit, ale doporučení vážených Moderátorů ↑ BrozekP: respektuji, proto opravdu prosím o nové téma.
Při cestách po Opavě samozřejmě buzolu nepoužívám, neboť se orientuji podle planet, ale pokud jsem kdy v životě provozovala byť velmi rekreáčně nějaký náznak sportu, tak to byl "orientační běh" (v mém případě "chůze") a plavání :-)
Balalajkove R´n´B, s textem se nemohu úplně souhlasit, ale hraje mi to tady, tak se podělím a budu pokračovat v plnění úkolu strany a vlady.
Jelikož takovou zbytečnosti se zaplaclo důležité téma chlapce z hájovny, tak na něho ještě upozorním - zejména od kolegů ze Slovenska se očekává reakce
Děkuji a mějte se.
Offline
Stránky: 1 2
- Hlavní strana
- » Ostatní
- » смесь математики для любителей русского n (TOTO TÉMA JE VYŘEŠENÉ)