Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 05. 2010 09:49 — Editoval jelena (08. 01. 2013 14:43)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Geometrie - konstrukční úlohy řešené na tomto fóru
Pokus o seřazení místních konstrukčních úloh.
Pokud máte zájem, můžete do tohoto tématu přidat svůj příspěvek, ve kterém si můžete pomoci EDITu udržovat seznam řešených úloh nebo dokazy. Děkuji.
Ulohy jsou v původním znění, bez úprav - občas jsem narazila na nekompletnost, na nepřesnosti, na nezodpovězený dotaz. Některé úlohy se nám opakuji. Snažila jsem přiřazit zadání k sbírkám "Planimetrie pro gymnázia", Petáková, případně Běloun (pro ZŠ). V případě cyklických záměn označení se mi to moc nedařílo - proto na úvod jsou úlohy "nezaměřeno".
Určitě je potřeba oprav, ani čeština není v pořádku - prosím o upozornění, opravím. Pokud je úloha nekompletní a někdo bude mít čas a náladu dořešit, tak samozřejmě děkuji.
Také děkuji všem autorům řešení a reakcí.
K zápisu konstrukce obecně Odkaz
Základní konstrukce: Odkaz
1) sestrojeni osy úsečky
2) osu uhlu
3) pravidelny sestiuhelnik
4) pravidelny petiuhlenik
5) kruznice trojuhelniku opsanou
6) kruznici trojuhelniku vepsanou
Dílo klasika.
Video konstrukcí trojúhelníku
Moc důkazů a geometrických konstrukcí - za odkaz děkuji kolegovi Olinovi.
Apolloniovy úlohy
Planimetrie pro SŠ.
Planimetrie pro SŠ
Planimetrie
Shodná zobrazení
Geometricke pojmy a ukazky konstrukcí (anglicky)
Geometrické pojmy a konstrukce (česky)
V ruštině (trojúhelník):
www.problems.ru - hodně řešených úloh (v ruštině)
Jakým způsobem přenést úsečku, úhel nebo trojúhelník? Odkaz
Co vznikne zlozenim 2 stredovych sumernosti alebo stredovej sumernosti a posunutia? Odkaz
Algebraické konstrukce, konstrukce algebraických výrazu, využití Pythagor. a Eukleid. věty, čtvrtá geometrická úměrná, redukční úhel:
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Přeměňte trojúhelník o stranách 6 cm, 5 cm a 3 cm ve čtverec o stejném obsahu.
***** Planimetrie pro gymnázia *****
2.6 Je dána kružnice m (S, 3 cm) a bod T, leží na m. Určete množinu středů tětiv TX kružnice m. Thaletova kružnice, tětiva je kolmá k poloměru, nejdélší tětiva je průměr. Odkaz
2.17 Najít na obvodu čtverce ABCD body, ze kterých je videt AC pod uhlem 100° Odkaz
2.19 a) |AB|=
 =6 cm,
=6 cm,  =5 cm,
=5 cm,  =5 cm (zadání: strana, těžnice na stranu, strana) Odkaz
=5 cm (zadání: strana, těžnice na stranu, strana) Odkaz2.19 c) |AB|=
 =6 cm,
=6 cm,  =5 cm,
=5 cm,  =5,5 cm (zadání: strana, výška na stranu, těžnice na stranu) Odkaz Odkaz
=5,5 cm (zadání: strana, výška na stranu, těžnice na stranu) Odkaz Odkaz2.19 d)
 ,
,  ,
,  (zadání: strana, výška na stranu, protilehlá úhel) Odkaz
(zadání: strana, výška na stranu, protilehlá úhel) Odkaz2.20 b)
 =60°,
=60°,  =5,5cm
=5,5cm  =|BC|=6 cm (zadání: úhel, těžnice, strana) Odkaz (nehotovo)
=|BC|=6 cm (zadání: úhel, těžnice, strana) Odkaz (nehotovo)2.20 b) BC=
 =5 cm,
=5 cm,  = 5.5 cm a uhel
= 5.5 cm a uhel  = 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz, Odkaz
= 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz, Odkaz2.20 c) BC=
 =5cm,
=5cm,  =3 cm,
=3 cm,  =5 cm (zadání: strana, výška na stranu, těžnice na jinou stranu) Odkaz
=5 cm (zadání: strana, výška na stranu, těžnice na jinou stranu) Odkaz2.20 b) BC=
 =5 cm,
=5 cm,  = 5.5 cm a uhel
= 5.5 cm a uhel  = 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz
= 60 stupňů (zadání: strana, těžnice na jinou stranu, úhel, návod: doplnění na rovnoběžník s úhlopříčkou u=2t_c). Odkaz2.20 d). Zadanou mám úsečku BC (5 cm), výšku na stranu b (vb=4,5 cm) a těžnici na stranu c (tc=5,5 cm) Odkaz, Odkaz
2.21 a)
 =4 cm,
=4 cm,  =5cm,
=5cm,  =5 cm (zadání: strana, výška na jinou stranu, těžnice na další stranu) (nehotovo) Odkaz
=5 cm (zadání: strana, výška na jinou stranu, těžnice na další stranu) (nehotovo) Odkaz2.21 b) trojúhelník, zadáno b=6cm, Výška na stranu b (Vb) = 1,5 cm Va 4 cm Odkaz
2.21 c) je dána úsečka |AA_0|=
 =4 cm, sestrojte všechny trojúhelníky ABC pro které platí
=4 cm, sestrojte všechny trojúhelníky ABC pro které platí  =6 cm,
=6 cm,  = 2,5 cm (strana, dvě výšky na zbývající strany) Odkaz
= 2,5 cm (strana, dvě výšky na zbývající strany) Odkaz2.22 b) Je dána úsečka |AA_1|=
 =6 cm, sestrojte všechny trojúhelníky ABC, pro které platí
=6 cm, sestrojte všechny trojúhelníky ABC, pro které platí  =8 cm,
=8 cm,  = 5 cm (zadání: strana, těžnice na stranu, výška na stranu) Odkaz
= 5 cm (zadání: strana, těžnice na stranu, výška na stranu) Odkaz2.22 c) je dána úsečka |AA_1| =
 = 6 cm, sestrojte všechny trojúhelníky ABC, pro které platí úhel
= 6 cm, sestrojte všechny trojúhelníky ABC, pro které platí úhel  =60°;
=60°;  = 4,5 cm (zadání: dvě těžnice, úhel) Odkaz
= 4,5 cm (zadání: dvě těžnice, úhel) Odkaz2.22 c) je dána úsečka AS, |AS|=
 =5 cm. Sestrojte všechny trojúhelníky ABC s těžnicí AS, pro které platí: těžnice
=5 cm. Sestrojte všechny trojúhelníky ABC s těžnicí AS, pro které platí: těžnice  = 8 cm, úhel
= 8 cm, úhel  = 30° (těžnice na stranu a, těžnice na stranu b, úhel) Odkaz
= 30° (těžnice na stranu a, těžnice na stranu b, úhel) Odkaz(překontrolovat).
2.22 c)
 ,
,  ,
,  (zadání : dvě těžnice, úhel) Odkaz
(zadání : dvě těžnice, úhel) Odkaz2.24)
 =75,
=75,  =3,5 cm,
=3,5 cm,  =2,5 cm (zadání: úhel, výška na protilehlou stranu, poloměr opsané kružnice) Odkaz, Odkaz, Odkaz, Odkaz
=2,5 cm (zadání: úhel, výška na protilehlou stranu, poloměr opsané kružnice) Odkaz, Odkaz, Odkaz, Odkaz2.25 – jiné označení)
 ,
,  ,
,  - poloměr kružnice vepsané (úhel, protiléhlá strana, poloměr kružnice vepsané) Odkaz
- poloměr kružnice vepsané (úhel, protiléhlá strana, poloměr kružnice vepsané) Odkaz(překontrolovat)
2.25) úhel
 = 45,
= 45,  =5 cm,
=5 cm,  poloměr kružnice vepsané (1,5cm) (zadání: úhel, protiléhlá strana, poloměr r kužnice vepsané) Odkaz, Odkaz, Odkaz
poloměr kružnice vepsané (1,5cm) (zadání: úhel, protiléhlá strana, poloměr r kužnice vepsané) Odkaz, Odkaz, Odkaz2.26 Sestrojte rovnostranný trojúhelník ABC, pro který platí r=3cm, kde r je poloměr kružnice opsané. Odkaz
2.28) pravoúhlý trojúhelník ABC s pravým vrcholem u C,
 =4,5 cm a
=4,5 cm a  poloměr vepsané kružnice=1,5 cm (pravoúhlý trojuhelník, odvěsná, poloměr vepsané kružnice) Odkaz Odkaz
poloměr vepsané kružnice=1,5 cm (pravoúhlý trojuhelník, odvěsná, poloměr vepsané kružnice) Odkaz Odkaz2.29 a), b) čtyřúhelníky (kosočtverce): Odkaz
a)
 = 3 cm,
= 3 cm,  =2v
=2vb)
 =4 cm,
=4 cm,  - poloměr vepsané kružnice je 1,5 cm
- poloměr vepsané kružnice je 1,5 cm 2.30 a) Sestrojte kosodélník ABCD, pro který platí: a=4cm,
 =60°, e=5,5cm. Odkaz
=60°, e=5,5cm. Odkaz2.30 b)Sestrojte kosodélník ABCD, pro který platí: e=5cm, f=3cm,
 =2,5cm. Odkaz
=2,5cm. Odkaz2.31 a) Sestrojte lichoběžník ABCD (AB || CD), pro který platí: b=4cm, v=3,5cm, e=8cm, f=7cm. Odkaz
2.31 b) Sestrojte lichoběžník ABCD (AB || CD), pro který platí: b=4cm, c=2cm,
 =60°,f=5cm. Odkaz
=60°,f=5cm. Odkaz2.32 b) Sestrojte čtyřúhelník ABCD, pro který platí: a=5cm, c=3cm,
 =75°, e=4,5cm, f=5,5cm. Odkaz
=75°, e=4,5cm, f=5,5cm. Odkaz2.33 a) Sestrojte tětivový čtyřúhelník ABCD, pro který platí: a=5cm,
 =120°, e=7cm, f=8cm. Odkaz
=120°, e=7cm, f=8cm. Odkaz2.33 b) Sestrojte tečnový čtyřúhelník ABCD, pro který platí: a=7,5cm, b=3,5cm,
 =45°,
=45°,  =2cm, kde
=2cm, kde  je poloměr kružnice vepsané. Odkaz
je poloměr kružnice vepsané. Odkaz2.33 c) Sestrojte dvojstředový čtyřúhelník ABCD, pro který platí:
 =60°,
=60°, =75°,
=75°, =2,5cm, kde
=2,5cm, kde  je poloměr kružnice vepsané. Odkaz
je poloměr kružnice vepsané. Odkaz2.35 a) Je dána úsečka AB (|AB|=6cm). Sestrojte všechny trojúhelníky ABC, pro které platí:
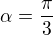 ,
,  = d cm, kde
= d cm, kde  . Odkaz
. Odkaz3.1 Odkaz
3.4 (konstrukce pomocí osové souměrnosti + výpočet]. Do daného čtverce ABCD, kde AB=a, je vepsán rovnostranný trojúhelník KLM tak, že K=A, L leží na BC, M leží na CD. Vyjádřete délku b strany rovnostranného trojúhelníku KLM pomocí délky a strany daného čtverce. Odkaz, Odkaz Odkaz
3.5 Je dána kružnice k(S;r) a bod M vně kružnice k. Sestrojte všechny rovnostranné trojúhelníky, pro něž je k kružnice vepsaná a bod M leží na přímce obsahující jednu stranu trojúhelníku. Odkaz
3.6 Sestrojte (bez použití úhloměru) rovnoramenný trojúhelník ABC, kde |AB|=6 cm je základna a
 = 105°. Odkaz
= 105°. Odkaz3.9 Odkaz Odkaz
3.11 Je dána přímka p a body A, B ležící v opačných polorovinách s hraniční přímkou p (AB není na p kolmá). Sestrojte na přímce p bod V tak, aby osa úhlu AVB ležela na přímce p. Odkaz Odkaz
3.12 Odkaz
3.14 Odkaz
3.15) sestrojit trojúhelník, dáno:
 =4 cm, úhel
=4 cm, úhel  = 60°,
= 60°, 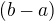 =1 cm (zadání: strana, přílehlý úhel, rozdíl stran, návod – osová souměrnost, symetrie) Odkaz
=1 cm (zadání: strana, přílehlý úhel, rozdíl stran, návod – osová souměrnost, symetrie) Odkaz3.15)
 ,
,  ,
,  (zadání: rozdíl stran, třetí strana, přílehlý úhel, návod: osová souměrnost, symetrie). Odkaz, Odkaz
(zadání: rozdíl stran, třetí strana, přílehlý úhel, návod: osová souměrnost, symetrie). Odkaz, Odkaz3.15 a)
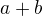 =10,
=10,  =5,
=5,  =3 (zadání: strana, součet stran (zbyvajících), výška, Odkaz
=3 (zadání: strana, součet stran (zbyvajících), výška, Odkaz 3.15 b) Odkaz
3.16 b) Sestrojte
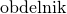 ABCD, je-li dáno
ABCD, je-li dáno  =7 cm,
=7 cm, 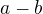 =1 cm (zadání: ondélník, rozdíl stran, uhlopříčka, návod: osová souměrnost) Odkaz
=1 cm (zadání: ondélník, rozdíl stran, uhlopříčka, návod: osová souměrnost) Odkaz3.17) sestrojit
 ABCD, dáno:
ABCD, dáno:  = 5 cm,
= 5 cm,  = 5.5 cm
= 5.5 cm  = 6 cm (přímka AC je osou souměrností deltoidu) (zadání: strana, úhlopříčky, deltoid, návod: osová souměrnost, symetrie). Odkaz
= 6 cm (přímka AC je osou souměrností deltoidu) (zadání: strana, úhlopříčky, deltoid, návod: osová souměrnost, symetrie). Odkaz 3.17 a) Odkaz
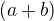 =10 cm,
=10 cm,  =6,2 cm,
=6,2 cm,  70 stupňů (zadání: strana, protilehlý úhel, součet stran (zbývajících), zdroj:- , návod: osová souměrnost, symetrie). Odkaz
70 stupňů (zadání: strana, protilehlý úhel, součet stran (zbývajících), zdroj:- , návod: osová souměrnost, symetrie). OdkazOdkaz
3.23 Odkaz
3.24b) Odkaz
3.28 a strana
 =4.2 cm, strana
=4.2 cm, strana  =5.3 cm a těžnice u strany
=5.3 cm a těžnice u strany  = 3.6 cm. Odkaz
= 3.6 cm. Odkaz3.28 b je dána úsečka AA1 (|AA1|= 5cm). Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí
 , a pro které platí:
, a pro které platí: 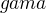 =45°,
=45°, 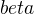 = 60° Odkaz
= 60° Odkaz3.28 c (stejný princip) úhel
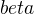 =60°, stranu AC=
=60°, stranu AC= =5 cm, a težnici
=5 cm, a težnici  =5 cm Odkaz, Odkaz
=5 cm Odkaz, Odkaz3.29 Odkaz
3.30 Odkaz
3.31 Odkaz
3.32 Odkaz Odkaz
3.33 Odkaz
3.35 Odkaz
3.36 Odkaz
3.38 Odkaz Odkaz
3.40 konstrukci rovnoběžníku, jestliže jsou dány: strana
 =5 cm, strana
=5 cm, strana  =3 cm a
=3 cm a  =úhel ASB (S je průsečík úhlopříček) má 120 stupňů. Odkaz, Odkaz posunutí
=úhel ASB (S je průsečík úhlopříček) má 120 stupňů. Odkaz, Odkaz posunutí3.41 Odkaz
Vzorový příklad 4, kap. Otočení dvě rovnoběžné přímky a, b, mimo ně bod C. Sestrojit rovnostranný trojúhelník ABC, aby vrcholy A, B ležely po řadě na přímkách a, b. Odkaz, Odkaz, Odkaz
3.50 Odkaz Odkaz
3.51 a) Jsou dány dvě soustředné kružnice
 (S, 4cm),
(S, 4cm), 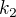 (S, 3cm) a bod A (|SA|=2cm). Sestrojte trojúhelníky ABC tak, aby B leželo na k1, C leželo na k2. Odkaz
(S, 3cm) a bod A (|SA|=2cm). Sestrojte trojúhelníky ABC tak, aby B leželo na k1, C leželo na k2. Odkaz3.51 b) Jsou dány dvě soustředné kružnice
 (S, 4 cm),
(S, 4 cm),  (S, 3 cm) a bod A (l SAl=2 cm). Sestrojte všechny čtverce ABCD tak, aby B ležel na k, D ležel na l. Odkaz
(S, 3 cm) a bod A (l SAl=2 cm). Sestrojte všechny čtverce ABCD tak, aby B ležel na k, D ležel na l. Odkaz3.53 Je dán bod
 , přímka
, přímka  a kružnice
a kružnice  (S, 3cm), vzdalenost |Sp|=4cm, |Cp|=2cm, |CS|=5cm, a body C, S leží v téže polorovině s hraniční přímkou p. Sestrojte všechny pravouhlé rovnoramenné trojuhelníky ABC ([hel u vrcholu C=90°) tak, aby A leželo na p, B leželo na k. Odkaz
(S, 3cm), vzdalenost |Sp|=4cm, |Cp|=2cm, |CS|=5cm, a body C, S leží v téže polorovině s hraniční přímkou p. Sestrojte všechny pravouhlé rovnoramenné trojuhelníky ABC ([hel u vrcholu C=90°) tak, aby A leželo na p, B leželo na k. Odkaz3.54 Jsou dány dvě nesoustředné kružnice
 (S, r1),
(S, r1),  (L, r2), r1 různý od r2, které se protínají v bodech C, Q. Sestrojte všechny rovnoramenné trojúhelníky ABC ( AB = základna), pro které platí A leží na k, B leží na l, úhel ACB = 120°. Odkaz
(L, r2), r1 různý od r2, které se protínají v bodech C, Q. Sestrojte všechny rovnoramenné trojúhelníky ABC ( AB = základna), pro které platí A leží na k, B leží na l, úhel ACB = 120°. Odkaz3.55 Odkaz
3.81[\b] Odkaz
[b]3.83 2.) Je dán čtverec ABCD strana
 =5cm a bod M uvnitř čtverce: M leží na BD, |MB|=2cm. Sestrojte všechny usečky XY, které mají krajní body X,Y na hranici čtverce tak, aby platilo |MX|:|MY|=4:3 Odkaz
=5cm a bod M uvnitř čtverce: M leží na BD, |MB|=2cm. Sestrojte všechny usečky XY, které mají krajní body X,Y na hranici čtverce tak, aby platilo |MX|:|MY|=4:3 OdkazVzorový - kapitola "Osová souměrnost" Je dán ostrouhlý trojuhelnik ABC. Uvnitř strany BC zvolte dva různé body P. Q. Na straně AB najděte bod X, tak aby součet |PX|+|QX| byl nejmenší. Odkaz
Vzorový - kapitola "Osová souměrnost" Daná je priamka p a v jednej z polrovín vyťatých priamkou p body A, B. Spomedzi bodov priamky p nájdite ten bod X, pre ktorý sa svetelný lúč idúci z bodu A do X odrazí od priamky p do bodu B (uhol odrazu sa rovná uhol dopadu). Odkaz
Vzorový příklad ke kapitole 3.7 Stejnolehlost - příklad 2 Ve Stejnolehlosti H(S,5/3) sestrojte obraz rovnoběžníku ABCD. Odkaz
Vzorový příklad 4 - kapitola 3.9 "Užití stejnolehlosti" Do trojúhelníku ABC vepište čtverec KLMN, KL náleží AB, M náleží BC, N náleží AC. Odkaz
Vzorový příklad 5 - kapitola 3.9 "Užití stejnolehlosti" dve různoběžky a bod M který leží někdě mezi nimi, ale ne na nich. mám vytvořit kružnice které se dotýkají bodu M i obou přímek..Odkaz
vzorový příklad 5 kap. Užití stejnolehlosti Jsou dány různoběžky a, b a bod C a. Sestrojte kružnici k, která se dotýká přímek b i a, té v bodě C. (R,P,K,D) http://forum.matweb.cz/viewtopic.php?id=17116 http://forum.matweb.cz/viewtopic.php?id=16964
Vzorový příklad 7 - kapitola 3.9 "Užití stejnolehlosti" jsou dány různoběžky a, b tak, že jejich průsečík P je nepřístupný (leží mimo papír), a bod K, který na nich neleží. Sestrojte přímku KP. Odkaz
3.86 a) Odkaz
3.86 b)
 = 5 cm,
= 5 cm,  = 2:3:4 (zadání: výška, poměr všech stran, další zdroj: Petáková, kapitola 10.9, úloha 72 e), návod: stejnolehlost)
= 2:3:4 (zadání: výška, poměr všech stran, další zdroj: Petáková, kapitola 10.9, úloha 72 e), návod: stejnolehlost) Odkaz
3.86 c) Odkaz
3.89 Dána polkruznica k(d=6cm) zostrojte stvorec ABCD. Vrcholy AB lezia na priemere a vrcholy CD na polkruznici. Odkaz
3. 110Sestrojte obecný čtyřúhelník ABCD dane je délky všech stran a,b,c,d (a>d) AC je osou uhla pri vrchole A. Odkaz
3.113 Jsou dány kružnice k1(S1;2,5cm), k2(S2;3cm), (/S2S2/=4cm) a <-> p (/S1p/ =5cm, /S2p/=4cm). Sestrojte <-> g rovnoběžnou s p, která vytíná na obou kružnicích shodné tětivy. Proveďte rozbor, zápis konstrukce, konstrukci a diskusi. Odkaz
3. 116 Odkaz Je dána kružnice k(S;r) a její dva poloměry SA, SB. Sestrojte tětivu kružnice k tak, aby byla oběma poloměry rozdělena na tři shodné úsečky.
Petáková:
kap. 10.4, ulohy 14 až 17 (je potřeba probrat :-) Odkaz Zadání, Řešení
kap. 10.4, uloha 15 a vc=5 cm c=3cm beta=120 [urlhttp://forum.matweb.cz/viewtopic.php?id=18695]Odkaz[/url]
kap. 10.4, úloha 18 a) použito jiné označení)
 =6.5 cm,
=6.5 cm,  =60°,
=60°,  =|BC|=6 cm (zadání: strana, strana, protilehlý úhel) Odkaz
=|BC|=6 cm (zadání: strana, strana, protilehlý úhel) Odkazkap. 10.4 úloha 18 e) , použito jiné otnačení)
 ,
,  ,
,  (zadání: strana, 2 těžnice na další strany) Odkaz, Odkaz Odkaz
(zadání: strana, 2 těžnice na další strany) Odkaz, Odkaz Odkazkap. 10.4, úloha 18 f) použito jiné označení ) Trojúhelník KLM:
 =5 cm,
=5 cm,  =9 cm,
=9 cm, 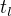 =6 cm (strana, dvě tečny) Odkaz, Odkaz, Odkaz
=6 cm (strana, dvě tečny) Odkaz, Odkaz, Odkazkap. 10.4, úloha 18 h) tři těžnice Odkaz, Odkaz
kap. 10.4, úloha 18 m)
 =9 cm,
=9 cm,  =7,5 cm,
=7,5 cm,  =6,5 cm (strana, těžnice na stranu, výška na jinou stranu) Odkaz
=6,5 cm (strana, těžnice na stranu, výška na jinou stranu) Odkazkap. 10.4, úloha 18 n)
 =6 cm,
=6 cm,  =5 cm
=5 cm  =4,5 cm (strana, výška na stranu, výška) Odkaz
=4,5 cm (strana, výška na stranu, výška) Odkazkap. 10.4, úloha 18q)
 ,
,  , úhel
, úhel  (zadání: strana, výška na stranu, protilehlý úhel, zdroj: Petáková, Odkaz, Odkaz
(zadání: strana, výška na stranu, protilehlý úhel, zdroj: Petáková, Odkaz, Odkazkap. 10.4, úloha 18 r)
 = 4 cm,
= 4 cm,  = 3 cm a
= 3 cm a  : a) 60 stupnu b) 120 stupnu (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
: a) 60 stupnu b) 120 stupnu (zadání: strana, těžnice na stranu, protilehlý úhel) Odkazkap. 10.4, úloha 18 r)
 ,
,  , úhel
, úhel  (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
(zadání: strana, těžnice na stranu, protilehlý úhel) Odkazkap. 10.4, úloha 18 r)
 =4 cm ,
=4 cm ,  =3 cm, úhel
=3 cm, úhel  =60˚ (zadání: strana, těžnice na stranu, protilehlý úhel) Odkaz
=60˚ (zadání: strana, těžnice na stranu, protilehlý úhel) Odkazkap. 10.4, úloha 18 r)
 ,
,  ,
,  (zadání: strana, protilehlý úhel, těžnice na jinou stranu, návod: středová souměrnost) Odkaz
(zadání: strana, protilehlý úhel, těžnice na jinou stranu, návod: středová souměrnost) Odkazkap. 10.4, úloha 18 s)
 ,
,  , úhel
, úhel  Odkaz, Odkaz těžnici na stranu a, těžnici na stranu c a úhel alfa. tc=3cm, uhol alfa 30stupnov, tb=7,5cm
Odkaz, Odkaz těžnici na stranu a, těžnici na stranu c a úhel alfa. tc=3cm, uhol alfa 30stupnov, tb=7,5cmkap. 10.4, úloha 18 u)
 =4 cm,
=4 cm,  =45,
=45,  = 60 (těžnice na stranu a úhly straně přilehlé), Řešení, Řešení Doplnit zdůvodnění.
= 60 (těžnice na stranu a úhly straně přilehlé), Řešení, Řešení Doplnit zdůvodnění.kap. 10.4, úloha 20 a)
 ,
,  ,
,  - poloměr kružnice vepsané (zadání: strana, přilehlý úhel, poloměr kružnice vepsané) Odkaz
- poloměr kružnice vepsané (zadání: strana, přilehlý úhel, poloměr kružnice vepsané) Odkazkap. 10.4, úloha 20 b)
 =4 cm,
=4 cm,  =60 stupnu,
=60 stupnu,  =1,5 cm (polomer kruz. vpisanej) (zadání: výska na stranu, úhel, poloměr kružnice vepsané Odkaz
=1,5 cm (polomer kruz. vpisanej) (zadání: výska na stranu, úhel, poloměr kružnice vepsané OdkazKapitola 10.4. zadání 21 a) dána úsečka ab, /AB/ =a.Sestrojte všechny rovnoběžníky ABCD, v nichž je dána výška va ke straně AB a /ASB/ =ω,kde průsečík uhlopříček je 0<ω< π [urlhttp://forum.matweb.cz/viewtopic.php?id=17855]Odkaz[/url]
kap. 10.4, úloha 23 b) Zostrojit
 , ak pozname dlzku jeho stran (
, ak pozname dlzku jeho stran ( ,
,  ), úhlopříčku
), úhlopříčku  a úhel ASB=120 stupňů, S - průsečík úhlopříček? Odkaz
a úhel ASB=120 stupňů, S - průsečík úhlopříček? Odkazkap. 10.4, úloha 23 c) Zostrojit
 , ak pozname dlzku jeho stran (
, ak pozname dlzku jeho stran ( ,
,  ,
,  ,
,  )? (lichoběžník, délka všech stran) Odkaz
)? (lichoběžník, délka všech stran) Odkaz10.6 41) Je dána úsečka OP= 4 cm, kružnice k(O; 2,5 cm), přímka p je kolmá na OP, P náleží p, bod M, kde OM=3 cm, úhel POM = 30°. Sestrojte všechny rovnoběžníky MOKL tak, aby K náleželo k, L nálaželo p. (řešení posunutím) Odkaz
10.6 42) Je dána úsečka OP= 4 cm, kružnice k(O; 2,5 cm), přímka p je kolmá na OP, P náleží p, bod M, kde OM=3 cm, úhel POM = 30° Sestrojte všechny rovnoramenné trojúhelníky ABC se základnou AB tak, aby B náleželo k, A náleželo p, vc je podmnožinou <-> PM, C = M. (řešení osovou souměrností) Odkaz
kap. 10.6, úloha 46 Je dána kružnice k (O, r=4 cm) a bod A (OA=3 cm). Sestrojte všechny tětivy XY kružnice k, které mají délku 6 cm a procházejí bodem A. Odkaz
Petáková, kap. 10.6, úloha 49 a), Odkaz, Odkaz
poloměr kružnice vepsané a velikost přepony v pravoúhlém trojúhelníku (4 řešení)
Odkaz
(nehotovo)
kap. 10.6, úloha 49 c) a+b+c=10cm alpha = 30stupnu beta = 45 stupnu. Odkaz, Odkaz
kap. 10.6, úloha 49 d) obvod
 =12cm,
=12cm,  =3cm, úhel
=3cm, úhel  60° (obvod trojúhelníku, výška, úhel) Odkaz, Odkaz
60° (obvod trojúhelníku, výška, úhel) Odkaz, Odkazkap. 10.9, úloha 62
1) Jsou dány 2 kružnice k1 (O, r=3,5 cm), k2 (S, r=2,5 cm), OS=7 cm. Sestrojte všechny přímky p tak, aby obě kružnice k1 i k2 vytínaly na přímce p stejně dlouhé tětivy délky 4 cm. Odkaz
úloha 65 Odkaz
úloha 68 Je dána kružnice k (S,r) a uvnitř ní bod M.Sestrojte všechny tětivy XY kružnice k, které procházejí bodem M tak, že bod M dělí tětivu XY v poměru 3:1. Odkaz
kap. 10.9, úloha 72 e),
 = 5 cm,
= 5 cm,  = 2:3:4 (zadání: výška, poměr všech stran, Zdroj: Planimetrie pro gymnázia, úloha 3.86 b), Petáková, návod: stejnolehlost)
= 2:3:4 (zadání: výška, poměr všech stran, Zdroj: Planimetrie pro gymnázia, úloha 3.86 b), Petáková, návod: stejnolehlost) Odkaz
kap. 10.9, úloha 72 a) Je dán trojúhelník ABC, velikost AC :BC je 5:4. velikost úhlu gama je 60 stupňů,výška na stranu c je 5 cm. Odkaz
kap. 10.9, úloha 72 g) poměr stran
 = 5:6:5,
= 5:6:5,  (poloměr kružnice vepsané) je 2 cm Odkaz
(poloměr kružnice vepsané) je 2 cm Odkazkap. 10.9, úloha 73 Do trojúhelníku ABC vepište čtverec KLMN, KL náleží AB, M náleží BC, N náleží AC. Odkaz
kap. 10.9, úloha 76 jsou dány různoběžky a, b tak, že jejich průsečík P je nepřístupný (leží mimo papír), a bod K, který na nich neleží. Sestrojte přímku KP. Odkaz
---------------------------------------------------------------------------------
VŠ
Řešení ze zadavacích listů - planimetrie:
1. Deltoid, zadáno dvě strany, poloměr kružnice vepsané.Odkaz
14. narysujte trojuhelnik ABC, je-li dano vyska na stranu c, teznice na stranu c, polomer kuznice vepsane - Odkaz
Strana
 , výška na stranu
, výška na stranu  , poloměr kružnice vepsané
, poloměr kružnice vepsané  - algebraická konstrukce Odkaz
- algebraická konstrukce OdkazVěčný trojuhelník
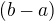 ,
,  - poloměr kružnice vepsané,
- poloměr kružnice vepsané,  Odkaz
OdkazÚlohy navazující na „věčný trojúhelník“ - zkonstruujte trojúhelník, je-li dáno:
a) obvod trojuhelniku
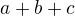 , výška na stranu
, výška na stranu  a úhel
a úhel  (zadáno: obvod trojúhelníku, součet všech stran, výška na jednu stranu, úhel protilehlý straně, zdroj: Petáková, kap. 10.6, úloha 49 d), návod: osová souměrnost, symetrie)
(zadáno: obvod trojúhelníku, součet všech stran, výška na jednu stranu, úhel protilehlý straně, zdroj: Petáková, kap. 10.6, úloha 49 d), návod: osová souměrnost, symetrie)b) rozdíl stran
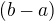 ,
,  poloměr kruznice opsané,
poloměr kruznice opsané,  kružnice vepsané,
kružnice vepsané, c) úhel
 , poloměr
, poloměr  kružnice opsané a poloměr
kružnice opsané a poloměr  kružnice vepsané. Odkaz
kružnice vepsané. Odkazd) sestrojte trojúhelník ABC, je-li dán vrchol C, dotyk T kružnice vepsané na straně AB a střed S strany AB Odkaz
Zdroj - nezaměřeno
*****************************Konstrukce trojúhelníků***********************
1.
 ,
,  a poměr výšek
a poměr výšek 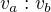 =3:2 (zadání: strana, těžnice na stranu, poměr výšek na zbývající strany) Odkaz
=3:2 (zadání: strana, těžnice na stranu, poměr výšek na zbývající strany) Odkaz2 a).
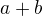 ,
,  ,
, 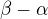 (což je kladné) (zadání: součet stran, třetí strana, rozdíl úhlů, návod: osová symetrie, souměrnost) Odkaz
(což je kladné) (zadání: součet stran, třetí strana, rozdíl úhlů, návod: osová symetrie, souměrnost) Odkaz2 b). součet stran a+b, strana c, úhel gama. Odkaz, Odkaz
3.
 =5 cm,
=5 cm,  =6 cm,
=6 cm,  =4,5 cm (zadání: dvě strany, těžnice na třetí stranu) Odkaz
=4,5 cm (zadání: dvě strany, těžnice na třetí stranu) Odkaz4.
 - poloměr kružnice vepsané, úhel
- poloměr kružnice vepsané, úhel  , strana
, strana  Odkaz, Odkaz (zdroj: Planimetrie pro gymnázia,úloha 2.25)
Odkaz, Odkaz (zdroj: Planimetrie pro gymnázia,úloha 2.25)(dodelat 2)
5. úhel
 60,
60,  =5 cm,
=5 cm,  =6 cm (zadání: úhel, výška, těžnice, návod: doplnění na rovnoběžník s úhlopříčkou u=2t), Odkaz
=6 cm (zadání: úhel, výška, těžnice, návod: doplnění na rovnoběžník s úhlopříčkou u=2t), Odkaz6. pravoúhlý trojúhelník, pravý úhel v bodě C, přepona
 = 4 cm, těžnice na stranu
= 4 cm, těžnice na stranu  = 2,2 cm (zadání: pravý úhel, přepona, těžnice na odvěsnou, návod: stejnolehlost) Odkaz
= 2,2 cm (zadání: pravý úhel, přepona, těžnice na odvěsnou, návod: stejnolehlost) Odkaz7.
 =4,2 cm
=4,2 cm  =30,
=30,  = 5cm (zadání: strana, přilehlý úhel, výška na stranu, zdroj: Běloun, Odkaz
= 5cm (zadání: strana, přilehlý úhel, výška na stranu, zdroj: Běloun, Odkaz8. úhel
 =45, |AB|=
=45, |AB|= =6 cm
=6 cm  =3 cm Odkaz
=3 cm Odkaz9. úhel
 ,
,  ,
,  (zadání: výška, těžnice na stejnou stranu, úhel straně protilehlý) Odkaz
(zadání: výška, těžnice na stejnou stranu, úhel straně protilehlý) Odkaz10.
 ,
,  ,
,  (strana, protilehlý úhel, těžnice na jinou stranu). Odkaz
(strana, protilehlý úhel, těžnice na jinou stranu). Odkaz11.
 ,
,  ,
,  (tři výšky) Odkaz, Odkaz, Odkaz, Odkaz, Odkaz
(tři výšky) Odkaz, Odkaz, Odkaz, Odkaz, Odkaz12.
 ,
,  ,
,  (zadání: výšky na dvě strany, těžnice na třetí stranu) Odkaz, Odkaz
(zadání: výšky na dvě strany, těžnice na třetí stranu) Odkaz, Odkaz13. poměr stran
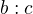 , úhel
, úhel  ,
,  (zadání: poměr stran, úhel, těžnice na třetí stranu, návod: stejnolehlost) Odkaz
(zadání: poměr stran, úhel, těžnice na třetí stranu, návod: stejnolehlost) Odkaz14.
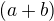 ,
,  , úhel
, úhel  (zadání: součet stran, úhel, třetí strana, návod: osová souměrnost, symetrie). Odkaz, Odkaz
(zadání: součet stran, úhel, třetí strana, návod: osová souměrnost, symetrie). Odkaz, Odkaz15 a) V rovnoramenném trojúhelníku ABC je |AC|=|BC|= 13cm a |AB| = 10cm. Pomocí podobnosti trojúhelníků vypočtěte poloměr kružnice vepsané a poloměr kružnice opsané. Odkaz
15 b) Zostroj rovnoramenný trojuholník ABC, ak poznáš vzdialenosť stredov kružnice vpísanej a opísanej (3 cm) a polomer kružnice vpísanej (4 cm). Odkaz
15 c) sestrojit trojúhelník, známe-li stranu a, poloměr kružnice opsané a vepsané. Odkaz
16.
 =130°,
=130°,  =4 cm,
=4 cm,  =2,2 cm. Odkaz
=2,2 cm. Odkaz17.
 ,
,  , trojúhelník pravoúhlý při vrcholu C Odkaz (nehotovo)
, trojúhelník pravoúhlý při vrcholu C Odkaz (nehotovo)18. Konstrukce trojúhelníku ABC, znám pouze: strany
 ,
,  , úhel
, úhel  (při vrcholu A) je větší než úhel beta (při vrcholu B). (původně chyba v zadání konstrukce trojúhelníku ABC, znám pouze: strany
(při vrcholu A) je větší než úhel beta (při vrcholu B). (původně chyba v zadání konstrukce trojúhelníku ABC, znám pouze: strany  ,
,  ; úhel
; úhel  (při vrcholu A) je větší než úhel beta (při vrcholu B). Odkaz
(při vrcholu A) je větší než úhel beta (při vrcholu B). Odkaz19.
 ,
,  (polomer kružnice vepsané),
(polomer kružnice vepsané),  . Odkaz, tento odkaz sem nepatří: Odkaz
. Odkaz, tento odkaz sem nepatří: Odkaz20. Sestrojte trojúhelník ABC, zname-li: bod A, prunik těžnic T, prunik os stran S (eulerová přímka)?? Odkaz
21.
 =8 cm,
=8 cm,  =5 cm, úhel
=5 cm, úhel  =75 stupňů Odkaz
=75 stupňů Odkaz22. poměr
 =5:4,
=5:4,  =60°,
=60°,  =5,5 cm Odkaz
=5,5 cm Odkaz23.
 ,
,  ,
,  (poloměr kružnice opsané). Sestroj trojúhelník ABC je- li dáno: úhel při vrcholu a je 60°, výška na stranu a je 6cm a poloměr kružnice opsané je 4cm. Odkaz Odkaz
(poloměr kružnice opsané). Sestroj trojúhelník ABC je- li dáno: úhel při vrcholu a je 60°, výška na stranu a je 6cm a poloměr kružnice opsané je 4cm. Odkaz Odkaz24.
 ,
,  ,
,  (dvě výšky, těžnice) Odkaz
(dvě výšky, těžnice) Odkaz25.
 =5cm, těžnice
=5cm, těžnice  =6 cm a vzdálenost těžiště od strany AB je
=6 cm a vzdálenost těžiště od strany AB je  =1,5 cm. Odkaz
=1,5 cm. Odkaz26.
 =5 cm,
=5 cm,  =6 cm,
=6 cm,  =6,5 cm (výška na stranu, těžnice na stranu, těžnice na jinou stranu) Odkaz
=6,5 cm (výška na stranu, těžnice na stranu, těžnice na jinou stranu) Odkaz27.
 =4 cm,
=4 cm,  =5 cm,
=5 cm,  =6 cm (dvě výšky, těžnice na třetí stranu) Odkaz
=6 cm (dvě výšky, těžnice na třetí stranu) Odkaz28. konstrukce rovnoramenného trojuhelníku (rameno a poloměr kružnice vepsané) - návrh konstrukce + důkaz, že ze zadaných rozměrů nejde sestrojit. Odkaz
29. ostroúhlý trojúhelník ABC. Sestrojte bod X tak, aby úhly AXB, BXC i CXA byly stejně velké. Odkaz
30. Sestrojte petiúhelník, znáte-li polohu pěti středů jeho stran. Odkaz
31. trojuhelník ABC, jestliže a = 6cm, uhel beta = 45*, teznice t_c = 5 cm Odkaz
33. Je dána úsečka B1B | B1B | = 4,8.Sestrojte všechny pravoúhlé trojúhelníky ABC,pro které je B1B těžnicí tb a pravý úhel je u vrcholu C.Jaké podmínky musí splňovat ta, aby existoval aspoň jeden trojúhelník uvedených vlastností? Odkaz
34. postup od Ivany(neumím vysvětlit, omluva), vysvětlila bych svůj text Odkaz
35. a+b=8cm, úhel a = 60°, vc=5 cm Odkaz
36. strana c=6cm, alfa=60 stupnů.těžnice t_b Odkaz
37. trojúhelník ABC, je-li dán úhel alfa, těžnice na stranu b a těžnice na stranu c. Odkaz
38. ťažnica na stranu a je 7, výška na stranu c je 4 a uhol alfa je 60 stupňov. Odkaz
39. BC-5cm, zostrojte trojuholnik ak plati AC-8cm tb-6cm-taznica b Odkaz
40. Užití stejnolehlosti - V rovině je dána přímka p a dvě soustředné kružnice k1(S,r1)a k2(S,r2), kde r1<r2. Sestrojte čtverec tak, aby dvě jeho protilehlé strany byly rovnoběžné s přímkou p. jedna z těchto dvou stran byla tětivou kružnice k2 a druhá z nich aby ležela na tečně ke kružnici k1. Zapište rozbor a popis konstrukce. Užijte stejnolehlosti. Odkaz
***********************Apolloniovy úlohy***************
1. Dane su dve sustredne kružnice k1(S,5cm)k2(S,2cm) a priamka p pre ktoru plati |Sp|=3cm .Zostrojte všetky kružnice , ktore sa dotykaju kružnic k1,k2 a priamky p. Odkaz
2. zostrojte všetky kružnice s polomerom 1,5 cm ktore sa dotýkaju danej kružnice k(S,4cm) a prechádzaju bodom M, pre ktorý platí |SM|=3cm b) |SM|=1cm c) |SM|=5cm Odkaz
3. Sestrojte kružnici, která se dotýká daných dvou různoběžek a prochází daným bodem, který leží uvnitř úhlu. Odkaz
******************Shodná a podobná zobrazení:********************
1. tri body A,B,C , jedna priamka, narysujte bod A tak, aby ležal na priamke p a vzdialenosti pB a pC sa rovnajú. Odkaz
2. Daná je úsečka AB a kružnica k. Zostrojte lichobežník ABCD, AB je rovnobežné s CD, /AB/= 3* /CD/ - AB je trojnásobok dĺžky CD, ak viete, že body C, D ležia na kružnici k. Odkaz
3. Daná je kružnica
 a body A, B. Zostrojte rovnobežník ABCD, ak viete, že body C, D ležia na kružnici k. Odkaz
a body A, B. Zostrojte rovnobežník ABCD, ak viete, že body C, D ležia na kružnici k. Odkaz4. Jsou dány dvě přímky p,q (různoběžné) a daný bod S (S neleží ani na jedné z nich). Sestrojte čtverec ABCD, tak že středem bude bod S a A \in p, C \in q. Odkaz
5. Uvnitř jedné poloroviny s hraniční přímkou p, jsou dány dvě kružnice k_1;k_2. Sestrojte všechny body P, z nichž lze vést ke k_1;k_2 tečny, takové že přímka p je osou jedné dvojice vrcholových úhlů, jimi sevřených. Odkaz
6. Narýsovat TEČNY KE KRUŽNICI k Z NEDOSTUPNÉHO VRCHOLU s využítím STEJNOLEHLOSTI. Odkaz
7 Je dána <-> p, kružnice k ( S;r) a úsečka AB. Sestrojte úsečku PU shodnou a rovnoběžnou s AB, aby P náleželo p a U náleželo k. Zvolte tak, aby úloha měla dvě řešení. Proveďte rozbor, zápis konstrukce, konstrukci a diskusi. Odkaz
8. Jsou dány přímky
 ,b,o (aje rovnoběžná s o, anení rovnoběžná s b) Sestrojte všechny rovnostranné trojúhelníky ABC s vrcholem A na přímce a,vrcholem B na přřímce b, jejichž těžnice tc je částí přímky o. Odkaz
,b,o (aje rovnoběžná s o, anení rovnoběžná s b) Sestrojte všechny rovnostranné trojúhelníky ABC s vrcholem A na přímce a,vrcholem B na přřímce b, jejichž těžnice tc je částí přímky o. Odkaz 9. Podobná zobrazení: Odkaz
10. úlohy od Ivanky schodná zobrazení (jsou chyby) Odkaz
11. Danému štvorcu ABCD vpíšte rovnostranný trojuholník, ktorého jeden vrchol leží na strane AB v danom bode X. Odkaz
12. Daný je štvorec ABCD a trojuholnik XYZ. Vpíšte do štvorca ABCD trojuholnik X'Y'Z' (vrcholy X', Y, 'Z' musia ležať na priamkach AB, BC, CD, DA) rovnoľahlý s trojuholnikom XYZ. Odkaz
13. Zostrojte trojuholnik ABC so stranami /AC/=6 cm, /BC/= 5cm, ak viete, že jeho ťažnice na strany AC a BC sú na seba kolmé. Odkaz
14. stejnolehlost - odkazy Odkaz
15. http://forum.matweb.cz/viewtopic.php?id=15235]Odkaz[/url]
V trojúhelníku ABC označíme AD osa úhlu při vrcholu A (D leží na straně BC), přičemž platí |BD|:|DC| = 2:1. Označíme ještě střed E strany AB.
a) V jakém poměru dělí os úhlu AD těžnice CE?
b) V jakém poměru dělí těžnice CE os úhlu AD?
16. V kruznici se stredem O jsou dva na sebe kolme prumery AB a CD a tetiva AM, ktera protina prumer CD v bode K. Pro jakou hodnotu uhlu BAM lze ctyruhelniku OBMK vepsat kruznici ??? Odkaz
17. Je dán ostroúhlý trojúhelník ABC. Sestrojte bod X tak, aby úhly AXB, BXC i CXA byly stejně velké. Odkaz
18. Jsou dány dvě kružnice
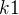 (S1, 3cm), k2(S2, 2 cm) a středná S1S2= 6 cm. Sestrojte přímku, která v první kružnici tvoří tětivu délky 5,5 cm a druhé se dotýká. Odkaz
(S1, 3cm), k2(S2, 2 cm) a středná S1S2= 6 cm. Sestrojte přímku, která v první kružnici tvoří tětivu délky 5,5 cm a druhé se dotýká. Odkaz******************************Důkazy a různé:*****************
podmínka, aby kružnice byla vepsanou a opsanou Odkaz
nevyřešeno: platí v rovnoramennom trojuholníku ABC s ramenami AC, BC táto veta ? "Os uhla ABC alebo BAC pretína rameno v bode, ktorý ho delí v pomere 1:2" Odkaz
Je možné po narysovaní takého trojuholníka a jeho kružnici vpísanej predĺžiť jeden polomer, ktorý je kolmý na rameno tak, aby tvoril výšku trojuholníka BXY, kde X leží na danom predĺženom polomere a Y leží na strane CB a trojuholník BXY je zhodný s trojuholník ABC ?
dokázat, že težiště, ortocentrum a průsečík os stran leží na jedné přímce. Odkaz
Žádné tři různé body téže přímky neleží na kružnici. Dokažte. Odkaz
Odkaz hodne
Odkaz konstrukční zápis
Odkaz důkaz
nevyřešeno MO V rovine je daný trojuholník PQX, pričom |PQ| = 3 cm, |PX| = 2,6 cm, |QX| = 3,8 cm. Zostrojte pravouhlý trojuholník ABC tak, aby sa jeho vpísaná kružnica dotýkala prepony AB v bode P, odvesny BC v bode Q a aby bod X ležal na priamke AC. Odkaz
V dané kružnici k sestrojte dva libovolné průměry AB, CD. Označte alfa úhel, který svírají přímky AB a CD. Dokažte, že tečny ke kružnici k v krajních bodech daných průměrů svírají také úhel alfa. Odkaz
daná je priamka
 a bod
a bod  , ktory na nej neleží. Zostrojte všetky kružnice, ktore prechádzaju bodmi A,C a dotýkajú sa priamky AB. Odkaz
, ktory na nej neleží. Zostrojte všetky kružnice, ktore prechádzaju bodmi A,C a dotýkajú sa priamky AB. OdkazDá sa zostrojiť rovnostranný trojuholník ABC, ak poznám obsah trojuholníka ASP, kde S je stred kružnice opísanej (alebo vpísanej) a P je stred strany AC Odkaz
přímka AB a na ní bod C. Najděte kružnici k tak, aby A leželo na k a C leželo také na k. Odkaz
Kruh o libovolném poloměru rozdělte kružnicí sním soustřednou na dvě části o stejných obsazích. Odkaz
Na konkretnom priklade popiste inverzne zobrazenie k zvolenemu zhodnemu zobrazeniu( otocenie, osova sumernost). Odkaz
důkaz v lichoběžníku Odkaz
Offline
#4 08. 11. 2010 21:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometrie - konstrukční úlohy řešené na tomto fóru
↑ BakyX: že by to tam nebylo, je to jeden z prvních konstrukčních postupů + početně. Nepořádek.
http://forum.matweb.cz/viewtopic.php?id=38492
http://forum.matweb.cz/viewtopic.php?id=18616
A na klíčové slovo "nehledala" jsem dohledala obrázek od IvanyOdkaz, děkuji.
Offline
#6 08. 11. 2010 23:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometrie - konstrukční úlohy řešené na tomto fóru
↑ BakyX: také děkuji :-)
Vyčlenila jsem téma v naději, že sem přibudou další příspěvky, ve kterých si můžete udržovat své seznamy (například s kolegou Spybotem hodně řešíte v Zajímavých. Pokud máte zájem, přidejte, prosím (i odkazy na nevyřešené).
Některé úlohy mám označeny, že nejsou vyřešeny. Jinak ten seznam je velmi nepřehledný, měla bych se posnažit více.
Offline
#7 09. 10. 2011 15:07 — Editoval janca361 (20. 11. 2011 13:38) Příspěvek uživatele janca361 byl skryt uživatelem janca361. Důvod: Všechny kontrukční úlohy zadané do sekce Základní škola před 9.10.2011
#8 09. 10. 2011 15:23 Příspěvek uživatele ((:-)) byl skryt uživatelem jelena. Důvod: vyřešeno
#9 09. 10. 2011 15:46 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: vyřešeno
#10 09. 10. 2011 15:50 Příspěvek uživatele janca361 byl skryt uživatelem jelena. Důvod: vyřešeno
#11 09. 10. 2011 15:58 Příspěvek uživatele janca361 byl skryt uživatelem jelena. Důvod: vyřešeno
#12 09. 10. 2011 16:01 — Editoval ((:-)) (09. 10. 2011 16:02) Příspěvek uživatele ((:-)) byl skryt uživatelem jelena. Důvod: OT
#13 09. 10. 2011 16:02 Příspěvek uživatele janca361 byl skryt uživatelem jelena. Důvod: OT
#14 09. 10. 2011 16:05 — Editoval ((:-)) (09. 10. 2011 16:11) Příspěvek uživatele ((:-)) byl skryt uživatelem jelena. Důvod: OT
#15 09. 10. 2011 16:23 Příspěvek uživatele jelena byl skryt uživatelem jelena. Důvod: OT
#16 09. 10. 2011 21:01 Příspěvek uživatele janca361 byl skryt uživatelem jelena. Důvod: OT
#17 01. 11. 2011 21:05 Příspěvek uživatele sedlajda byl skryt uživatelem janca361. Důvod: V novém tématu
#18 01. 11. 2011 21:15 Příspěvek uživatele janca361 byl skryt uživatelem janca361.
#19 01. 11. 2011 21:20 Příspěvek uživatele sedlajda byl skryt uživatelem janca361.
#20 01. 11. 2011 21:23 Příspěvek uživatele janca361 byl skryt uživatelem janca361.
#21 20. 11. 2011 14:55 — Editoval janca361 (20. 11. 2011 14:57)
- janca361

- .
- Příspěvky: 3284
Re: Geometrie - konstrukční úlohy řešené na tomto fóru
Pěkné nedělní odloledne všem,
hlásím, že jsem dokončila sbírku úloh pro ZŠ. Docela jsem si pohrála ;)
Jak to uspořádat, aby se v rom dalo hledat? Mě se docela líbí to, jak navrh Olin a odkázala ↑ jelena:, ale netuším, co některé značky v EN znamenají. Nějaké jiné návrhy?
EDIT:
Jo, a pokud narazíte na chyby opravujte rovnou ;) nebo hlaště ;) Díky.
Offline
#22 12. 12. 2011 00:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometrie - konstrukční úlohy řešené na tomto fóru
↑ janca361:
trochu opožděně - gratulace k seřazení (seřazení dle vzoru kolegy Olina je pohodlnější na MatWiki :-)
Janča v jiném tématu napsal(a):
ale čekala jsem, že to bude seřazené
:-) seřadila jsem 3.4 a 3.15 (ale také jsem se dočetla, že Tobě při hledání chyběla čárka - dbám na zákony zachování - pokud mi někde chybí čárka, jinde přebývá - např. v párku.
Zdravím.
Offline
#24 28. 01. 2012 21:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Geometrie - konstrukční úlohy řešené na tomto fóru
↑ zrzsat:
musí to někde být :-)
Pokud je  - poloměr kružnice opsané, potom využíváš vlastnost středového a obvodového úhlu a nejdřív sestrojuješ pomocný trojúhelník - rovnoramenný, rameno=r, úhel u vrcholu=2*alfa, základna bude strana
- poloměr kružnice opsané, potom využíváš vlastnost středového a obvodového úhlu a nejdřív sestrojuješ pomocný trojúhelník - rovnoramenný, rameno=r, úhel u vrcholu=2*alfa, základna bude strana  .
.
Ze středu strany a sestrojíš těžnici a nad stranou a množinu bodu, ze kterých vidíme stranu  pod úhlem alfa.
pod úhlem alfa.
Stačí to tak na úvod? Příště si prosím, založ nové téma (viz. pravidla). Děkuji a zdravím.
Offline
#25 14. 11. 2012 19:44
- janca361

- .
- Příspěvky: 3284
Re: Geometrie - konstrukční úlohy řešené na tomto fóru
Shromažďuju v oblíbených co se nám na foru za poslední rok urodilo. Nevím, kolik mi toho uniklo, ale snad mnoho ne.
Už se toho docela dost namnožilo a tak to hodím sem, třeba to někdy zařadím (nebo někdo zařadí), případně zůstane nezařazeno.
Konstrukce trojúhelníků
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Konstrukce čtyřúhelníku Odkaz
Konstukce rovnoběžníku Odkaz
Konstrukce kosodélníku Odkaz
Konstrukce lichoběžníků
Odkaz
Odkaz
Odkaz
Odkaz
Shodná zobrazení
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Stejnolehlost
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Odkaz
Nezařeneno
Odkaz
Pythagorova věta Odkaz
Množina bodů dané vlastnosti
Odkaz
Odkaz
Odkaz
Redukční úhel
Odkaz
Offline

 ,
, 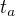 a r. Děkuji za odpověď.
a r. Děkuji za odpověď.